問３解答

問題に戻る

＜解説＞

まず問題の（図１）の三角形の面積を求めましょう。

（図Ａ）

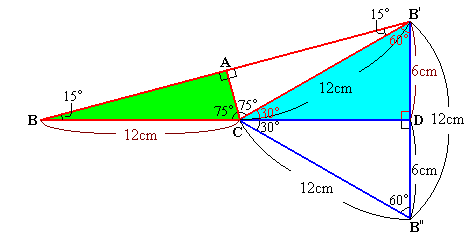
（図Ａ）で、三角形ＡＢＣの面積を求めるわけですが、この三角形を辺ＡＣを折り目としてひっくり返して三角形ＡＢ'Ｃを作ると、三角形Ｂ'ＢＣは３つの角がそれぞれ１５度、１５度、１５０度の二等辺三角形です。
（図Ａ）で三角形Ｂ'ＢＣの底辺をＢＣとすると、高さはＢ'Ｄにあたります。
ここで三角形ＣＢ'Ｄは３つの角度がそれぞれ３０度、６０度、９０度の直角三角形です。
この直角三角形ＣＢ'Ｄにおいて、一番短い辺と一番長い辺の長さの比は１：２となります！これは、三角形ＣＢ'ＤをＣＤを折り目としてひっくり返して三角形ＣＢ"Ｄを作ると三角形ＣＢ'Ｂ''が正三角形になることからわかります。
ＣＢ'＝１２ｃｍなので、ＤＢ'＝６ｃｍ。よって三角形ＢＢ'Ｃの面積は１２×６÷２＝３６cm²。
三角形ＡＢＣの面積は三角形ＢＢ'Ｃの面積の面積の半分だから３６÷２＝１８ｃｍ²。

次に問題の（図２）において、三角形をずらした長さを考えます。

（図Ｂ）

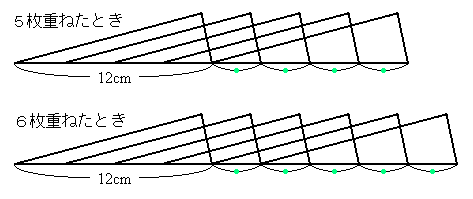
（図Ｂ）のように、簡単な例で考えると、５枚のとき、底辺の長さは１２ｃｍ＋「等しい長さ」が４つ、ここにもうひとつ三角形を重ねると（すなわち、６枚重ねたとき）、底辺の長さは１２ｃｍ＋「等しい長さ」が５つとなり、「等しい長さ」が１つ増えます。
このことから、「等しい長さ」の数は重ねた三角形の枚数よりも１だけ少ないことがわかります。
ここでは三角形を４５枚重ねたのだから底辺の１４４ｃｍは、１２ｃｍ＋「等しい長さ」が４４個からなっています。
よって、「等しい長さ」の１つの長さは（１４４−１２）÷４４＝３ｃｍです。

さて、いよいよ３重になった部分の面積を求めます。

（図Ｃ₁）

（図Ｃ₂）

（図Ｂ）のときと同じく簡単な例で考えます。（３重になっている部分の形としては（図Ｃ₂）のア、イ、ウの３通りあります）
５枚のとき３重になっている部分は（図Ｃ₂）のアが１個、イが１個、ウが１個。ここにもうひとつ三角形を重ねると（すなわち、６枚重ねたとき）３重になっている部分は（図Ｃ₂）のアが１個、イが２個、ウが１個となり、イだけが１個増えます。
このことから、３重になっている部分はアとウは各１個、イは重ねた三角形の数よりも４だけ少ないことがわかります。
ここでは三角形を４５枚重ねたのだからアとウは各１個、イは４１個あるとわかります。

（図Ｄ）

次にア、イ、ウの面積を求めます。（図Ｄ）のように、三角形を１６等分すると、アとウは小三角形３個分、イは小三角形２個分です。
小三角形１個の面積は１８÷１６＝９／８ｃｍ²だから、アとウは９／８×３＝２７／８ｃｍ²、イは９／８×２＝９／４ｃｍ²。
よって、３重になっている部分の面積は、２７／８×２＋９／４×４１＝３９６／４＝９９ｃｍ²。

問題に戻る