![]() 問4の解答
問4の解答
<解説>
厚紙の模様を考えずに合同な正三角形の厚紙を4+21=25枚使うと、(図1)のような正三角形ができます。
(図1)
さて、ここで「模様が線対称」とはどういうことかを考えます。
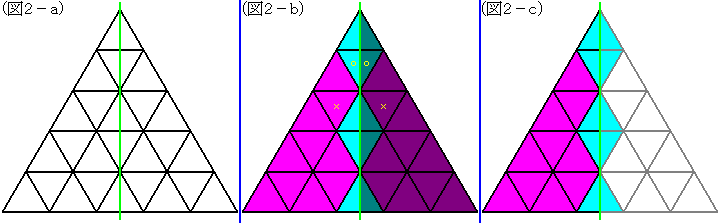
まず(図2−a)のように対称軸を引いてみます。
“線対称”ですから、軸より左側の模様と軸より右側の模様は同じでなければいけません。((図2−b)参考)
つまり、軸より左側の模様を決めれば、軸より右側の模様はただ1通りに決まります。
結局は、(図2−c)において色をつけた15個の三角形だけを考えればよいことがわかります。
厚紙の置き方を表にしたのが下の表です。
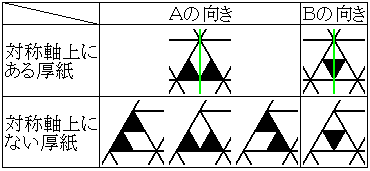
対称軸上にある5枚は対称軸より左側と右側の模様が一致しなければならないので2種類の厚紙の置き方は1通りしかありません。
対称軸上にない10枚(左側のみ)は向きは関係なく、どんなに置いてもいいですから、Aの置き方は3通り、Bの置き方は1通りです。
なお、厚紙を下向きに置く場合も上の表と同様です。
ここでAの厚紙4枚を、「対称軸上にある部分」と対称軸上にない部分の左側のみにどのように置けばいいかを考えます。
対称軸上でない部分の左側に1枚置くと、軸に対して反対側に1枚置かなければなりません。(“線対称”ですから)
よって、Aの置き方としては、
(1)対称軸上でない部分の左側に2枚(=対称軸上でない部分に4枚)、対称軸上に0枚
(2)対称軸上でない部分の左側に1枚(=対称軸上でない部分に2枚)、対称軸上に2枚
(3)対称軸上でない部分の左側に0枚、対称軸上に4枚
の3パターンが考えられます。
ただし、“順列”ではなく“組み合わせ”で考えなければいけないことに注意してください。
また、AかBのどちらかの置く場所をすべて決めれば、残りの厚紙の置く場所が決まるということがわかります。
(1)の場合、
対称軸上でない部分の左側の10箇所:10箇所にA2枚を置く組み合わせは10×9÷(2×1)=45通り。
Aの向きを考えると2枚とも前の表で3通りの置き方があるとわかっているので45×3×3=405通り。
対称軸上の5箇所:これはすべてBを置くことになるのでただ1通りしかありません。
よって、405×1=405通り。
(2)の場合、
対称軸上でない部分の左側の10箇所:10箇所にA1枚を置く組み合わせは10通り。Aの向きを考えると10×3=30通り。
対称軸上の5箇所:5箇所にAを2枚置く組み合わせは5×4÷(2×1)=10通り。
よって、30×10=300通り。
(3)の場合、
対称軸上でない部分の左側の10箇所:すべてBを置くことになるのでただ1通り。
対称軸上の5箇所:Aを4枚置く組み合わせよりもBを1枚置く組み合わせと考えたほうが簡単で、5通り。
よって、1×5=5通り。
以上より、405+300+5=710通り。
細かいことですが、問題では「何種類?」と聞かれているので、「…通り」を「…種類」に直しておいた方がいいでしょう。
正解;710種類 |