![]() 問5解答
問5解答
<解説>
展開図を組み立てたときの形を知ることさえ困難な超難問です。
立体の形がわかったとしても、体積を求めることは決して容易ではありません。
では、まず第一目標の、立体を描くことからです。(図1−a)を見てください。
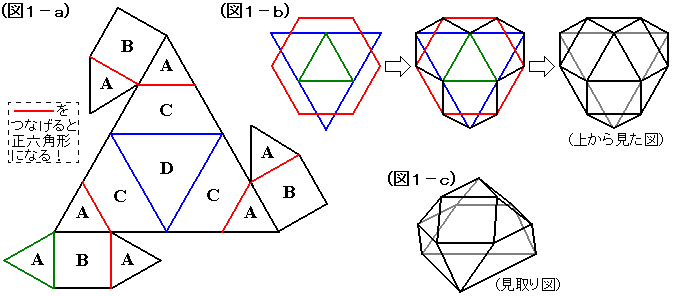
Dの面(青で囲った部分)を底面にします。このとき、一番上にくる面はA(緑で囲った部分)になることはすぐ見当がつくと思います。
次に、赤く色をつけた部分に注目します。
この赤い線をつなぐと正六角形になるということがわかりますか?
厳密に説明すると大変なことになりそうなので省略しますが(^-^;、Dの面の辺と平行になることなどから判断できます。
これらを利用して上から見た図を書いてみます(図1−b)。
青で囲ったDの面、Dを底面にした時一番上にくる緑で囲ったAの面、そして赤く色をつけた正六角形を空間に置き、あとはこれに面をはめこんでいけばいいです。
これで上から見た図ができあがりました。
これをもとにして描いた見取り図が(図1−c)です。
(図1−c)を見る限り、このままでは体積を求められそうにありません。
そこで下の(図2)のように、立体を2つに分割して、それらの体積を別々に求めることにします。
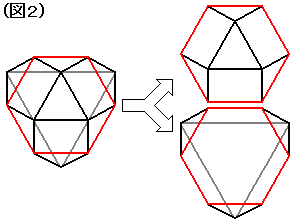
まず(図2)で分けた立体のうち、上の方の立体の体積から求めましょう。
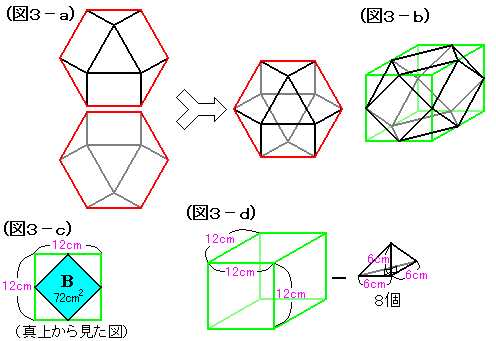
同じ立体をもうひとつ用意し、正六角形の面でくっつけます(図3−a)。
うまくくっつけると、(図3−b)のように、立方体の中に埋めこむことができます!
では、(図3−b)の立方体の一辺の長さを求めます。
(図3−c)は、(図3−b)を上から見たものです。
Bの面の頂点は、立方体の辺の真ん中の点を結んだものになりますから、Bの対角線の長さ=立方体の一辺の長さですね。
正方形は、ひし形の特殊なものですから、ひし形の面積の公式((対角線)×(もう一方の対角線)÷2)を使うと、面積は
(Bの対角線)×(Bの対角線)÷2=72、すなわち(Bの対角線)×(Bの対角線)=144となります。
144=12×12ですから、立方体の一辺の長さは12cmです。
(図3−b)の立体の体積は(図3−d)のようにして求められます。
よって、12×12×12−(6×6÷2×6÷3)×8=1440cm3
これは実際の立体を2つくっつけたものの体積なので、これを2で割って、
1440÷2=720cm3 …(ア)
次に、(図2)で分けた立体のうち、下の方の立体の体積を求めましょう。
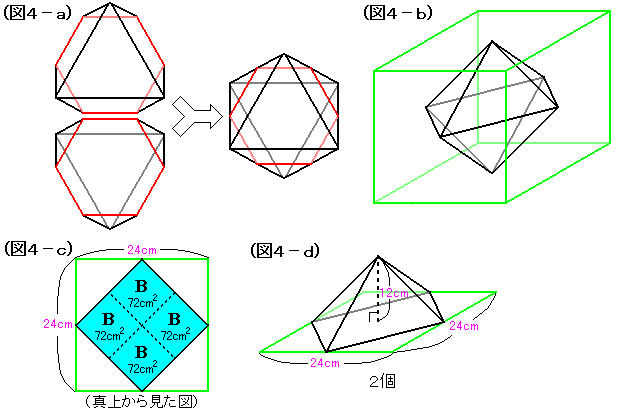
先ほどと同じように、同じ立体をもうひとつ用意し、正六角形の面でくっつけます(図4−a)。
うまくくっつけると、正八面体ができます。
この正八面体の体積は、(図4−b)のように、やはり立方体に埋め込んでみるとわかりやすいです。(正八面体の頂点は、立方体の各面の中心にあります)
では、(図4−b)の立方体の一辺の長さを求めます。
(図4−c)は、(図4−b)を上から見たものです。
正八面体の一辺の長さは、Dの面の一辺の長さ、つまり、Bの面の一辺の長さの2倍です。
立方体の一辺の長さもBの面の対角線の長さの2倍となりますから、立方体の一辺の長さは12×2=24cmです。
(図4−b)の立体の体積は、四角すい2個に分けて体積を求めます(図4−d)。
(24×24÷2×12÷3)×2=2304cm3
これは実際の立体を2つくっつけたものの体積なので、これを2で割って、
2304÷2=1152cm3 …(イ)
(ア)(イ)から、720+1152=1872cm3
正解;1872cm3 |