問７（算トラ２出題候補）解答

問題に戻る

＜解説＞

ＣＤを底辺とした時の高さを求めればいいわけですが、そう簡単には求まってくれません。

まずは（解説図）をご覧ください。

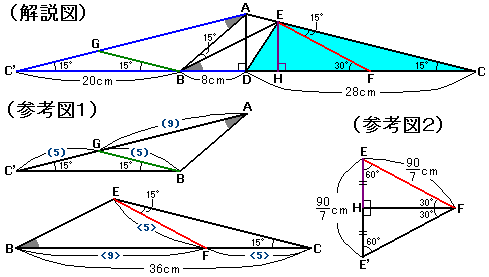
どんな補助線を引いたかというと…
三角形ＡＤＣをＡＤを軸として折り返して三角形ＡＤＢ'を作り（図の青い線）、角ＣＥＦ＝１５度となるような点ＦをＣＤ上にとってＥとＦを結び（図の赤い線）、角Ｃ'ＢＧ＝１５度となるような点ＧをＡＣ'上にとってＢとＧを結びます（図の緑の線）。
求めたいのはＥＨの長さです（図の紫の線）。

青い線の引き方からＣ'Ｄ＝ＣＤなので、Ｃ'Ｃ＝２８×２＝５６ｃｍ、Ｃ'Ｂ＝２８−８＝２０ｃｍです。

三角形ＡＣ'Ｃと三角形ＧＣ'Ｂは、等しい２つの角度が１５度の二等辺三角形ですから、相似ですね。
相似比はＣ'Ｃ：Ｃ'Ｂ＝５６：２０＝１４：５ですから、ＡＣ'：ＧＣも１４：５となります。
したがって、ＡＧ：ＧＣ'＝（１４−５）：５＝９：５です。

次に三角形ＡＢＣ'と三角形ＢＥＣを考えると、この２つの三角形は相似です。
角ＡＣ'Ｂ＝角ＢＣＥ＝１５度は一目瞭然ですが、あと１組の角が等しいことには少し気付きづらいでしょうか。
角ＢＡＣ'＝１８０度−１５度×２−角ＢＡＥ＝１５０度−角ＢＡＥ　（三角形ＡＣＣ'で考えた）、
一方、角ＥＢＣ＝１８０度−１５度×２−角ＢＡＥ＝１５０度−角ＢＡＥ（三角形ＡＢＣで考えた）。
よって角ＢＡＣ'＝角ＥＢＣがいえました。

ここで（参考図１）を見てください。三角形ＡＢＣ'と三角形ＢＥＣを取り出したものです。
上の方の図は"三角形ＡＢＣ'において、角Ｃ'ＢＧ＝１５度となる点ＧをとるとＡＧ：ＧＣ'＝９：５となった"というように見ることができます。
三角形ＡＢＣ'と相似な三角形ＢＥＣでも同様に、角ＣＥＦ＝１５度となるような点Ｆを取るとＢＦ：ＦＣ＝９：５となりますよね。

ＢＣ＝２８＋８＝３６ｃｍですから、ＣＦ＝３６×５／（９＋５）＝９０／７ｃｍ。
ＦＣ＝ＦＥなので、ＦＥ＝９０／７ｃｍです。

三角形ＥＨＦに注目すると、ＥＦ：ＥＨ＝２：１ですから、ＥＨ＝９０／７×１／２＝４５／７ｃｍです。
なぜＥＦ：ＥＨ＝２：１になるかは…（参考図２）を見てください。
三角形ＥＨＦを、ＨＦを折り目として三角形Ｅ'ＨＦを作ると、三角形ＥＥ'Ｆは正三角形になることからわかります。

というわけで、三角形ＣＤＥの面積は
２８×４５／７÷２＝９０ｃｍ²

#これはある方から寄せられた解法です。
私の想定していた解法より素晴らしいものであったので紹介してみました。

え…？私の解法ですか…？
……こちらです。
この図で本格的に説明しようとしたら画像が巨大なものになってしまったので参考までにとどめておきます(^^;

問題に戻る