![]() 問9の解答
問9の解答
<解説>
まずは面積を3等分する点はどこにあるかを調べます。下の図をご覧ください。
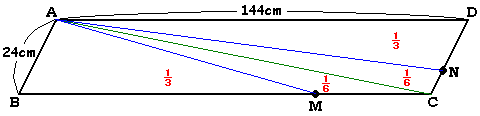
三角形ABCと三角形CDAは、3辺の長さがそれぞれ等しいので合同ですから、平行四辺形の面積を1とすると、三角形ABCと三角形ACDの面積は両方とも1/2です。
点Aと結ぶ直線によって平行四辺形の面積を3等分する点の内ひとつはBC上(ここにとる点をMとする)、もうひとつはCD上(ここにとる点をNとする)にあります。
すると、三角形ABMの面積は1/3、三角形ADNの面積も1/3です。
三角形ACMの面積は三角形ABCから三角形ABMを除いたものなので、1/2−1/3=1/6、三角形ACNの面積は三角形ACDから三角形ADNを除いたものなので、やはり1/2−1/3=1/6となります。
三角形ABMと三角形ACMは、底辺をそれぞれBM,CMとすると、高さは共通ですから、底辺の比は面積の比に等しく(いわゆる“等高底比(とうこうていひ)”です)、BM:CM=1/3:1/6=2:1となるので、BM=144×{2/(2+1)}=96cm、CM=144−96=48cmです。
一方、三角形ADNと三角形ACNは、底辺をそれぞれDN,CNとすると、さっきと同様に“等高底比”からDN:CN=1/3:1/6=2:1ですから、DN=24×{2/(2+1)}=16cm、CN=24−16=8cmです。
AとP、AとQを結んだ直線によって、平行四辺形の面積が3等分される可能性があるのは、
(Case1)点Pが点Mに一致したときにちょうど点Qが点Nに一致したとき
(Case2)点Pが点Nに一致したときにちょうど点Qが点Mに一致したとき
の2ケースです。
平行四辺形の1周の長さは(144+24)×2=336cmなので、
点Pは、336÷8=42秒で1周し、点Qは336÷15=22.4秒で1周します。
(Case1)
点Pがはじめて点Mに一致するのは、(24+96)÷8=15秒後であり、その後1周するたび;つまり42秒ごとに点Mに一致します。
よって、その時間は 15,57,99,141,183,225,……秒 です。
一方、点Qがはじめて点Nに一致するのは、(24+144+8)÷15=176/15秒後で、その後1周するたび;つまり22.4=112/5=336/15秒ごとに点Nに一致します。
よって、その時間は、初歩的な「文字と式」で(176+336×A)/15秒と表せます(Aは0以上の整数)。
176は3の倍数ではありませんが、336は3の倍数ですので、分子(176+336×A)は3の倍数ではありません。しかし、分母(15)は3の倍数です。よって、(176+336×A)/15は3で約分できないので、これは整数になりません。
でもPがMに一致する時間というのは必ず整数ですから、点PがMに一致したときににちょうど点QがNに一致することはありえません。
(Case2)
点Pがはじめて点Nに一致するのは、(24+144+8)÷8=22秒後であり、その後1周するたび;つまり42秒ごとに点Nに一致します。
よって、その時間は 22,64,106,148,190,232,……秒です。 …(※)
点Qがはじめて点Mに一致するのは、(24+96)÷15=8=40/5秒後であり、その後1周するたび;つまり22.4=112/5秒ごとに点Mに一致します。
よって、その時間は、初歩的な「文字と式」で(40+112×B)/5秒と表せます(Bは0以上の整数)。
点Pがはじめて点Nに一致する時間は整数ですから、点Qが点Mに一致する時間が整数でなければいけません。そのためには40+112×Bが整数でなければいけません。40は5の倍数ですから、112×Bも5の倍数でなければいけません。112は5の倍数ではないので、Bは0か、あるいは5の倍数であればいいですね。
そこでBに0,5,10,15,… を当てはめていくと、8,120,232,344,……秒となり、(※)と共通するもののうち最小の232秒が答えです。
正解;232秒後 |