![]() 問10の解答
問10の解答
<解説>
問題文の「ある整数(333を割る数)」をAとすると、問題文にある式は、
333÷A=….……7494………
と表せます。 「…」の部分は、どんな数字が来るかはわかりません。
この式に10を何回かかけて、7494が小数点の直前に来るようにしてみましょう(10を1回かけるごとに、小数点は右にひとつずれます)。
333×10・・・0÷A=……….7494………
右辺の整数部分をBとすると、
333×10・・・0÷A=B.7494………=B+0.7494………
と表せ、さらに両辺にAをかけると、
333×10・・・0=(B+0.7494………)×A=A×B+A×0.7494………
これを変形する(両辺からA×Bを引く)と、
333×10・・・0−A×B=A×0.7494………
となります。
上の式で、AもBも整数ですから、A×Bも整数です。 ですから、333×10・・・0−A×Bも整数です。
よって、A×0.7494………も整数となります。
0.7494………という数字は、0.7494以上0.7495未満ということです。
結局、A×0.7494以上A×0.7495未満に整数があるようなAを見つければよいことがわかります。 …(◆)
0.7494=0.75−0.0006
; 0.7495=0.75−0.0005 と変形(実はこの変形がポイント!)してから、下のような表を作ります。
ここで、Pは「0.75×Aより小さい整数のうち最大である数」とします。
(表X)
| A | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | …… |
| 0.75×A | 0.75 | 1.5 | 2.25 | 3 | 3.75 | 4.5 | 5.25 | 6 | 6.75 | 7.5 | …… |
| P | 0 | 1 | 2 | 2 | 3 | 4 | 5 | 5 | 6 | 7 | …… |
| 0.75×A−P | 0.75 | 0.5 | 0.25 | 1 | 0.75 | 0.5 | 0.25 | 1 | 0.75 | 0.5 | …… |
0.75×A−Pの値は、 0.75→0.5→0.25→1→… と、周期的に変わっていることがわかります。 …(★)
さて、(◆)や(表X)を参考にすると、「A×0.7494以上A×0.7495未満に整数Pがある」という状態は次のようなときです。
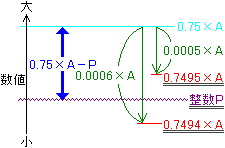
この図を見ると、0.0006×Aは0.75×A−P以上でなければいけません。
0.75×A−Pの値は(★)より0.25以上ですから、0.0006×Aが0.25以上になるには、
0.25÷0.0006=416.666……
より、Aは417以上である必要があります。
しかし(★)および(表X)を見ると、0.75×A−Pの値が0.25になるのは、Aが3,7,11,…(4で割ると3あまる数)のときですから、417以上の整数で4で割ると3あまる数のうちもっとも小さいのは419です(417÷4=104
あまり1 ですから、417にあと2足せばあまりは3になりますね)。
実際に調べてみると、
419×0.7494=313.9986
419×0.7495=314.0405
となり、419×0.7494以上419×0.7495未満に確かに(314という)整数があります!
というわけで、答えは419!! …でもちょっと待って下さい。これは現時点では「答えの有力候補」にすぎません。
本当にこれが答えであるのか確かめてみましょう。333を419で割ってみます。
333÷419=0.79474940……
確かに7494が出てきましたから、これで419が答えであるとわかりました。
正解;419 |