![]() 問11(算トラ3出題候補問題)の解答
問11(算トラ3出題候補問題)の解答
<解説>
台形の面積の公式 (<上底>+<下底>)×<高さ>÷2 は、(算数的には)使えません。
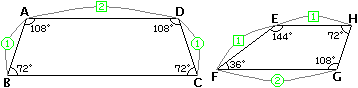
準備として、問題文の条件通りの長さを記した上のような図を用意しておきます。
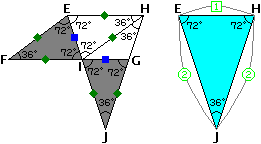
さて、まずは台形EFGHに注目してみます。
角Eを二等分するような直線を引き、FGとの交点をIとし、また、HGの延長線との交点をJとします(下の左の方の図)。
三角形EJHを見ると、角EJH=180度−72度×2=36度となります。 …(1)
三角形EIFと三角形EIHは合同です(EIは共通、EF=EH、角IEF=角IEH だから、「2辺とその間の角がそれぞれ等しい」)。
よって、IF=IH …(2)
また、角EHI=36度から、角IHJ=72度−36度=36度です。 …(3)
ここで、三角形HIJを見ると、(1)(3)より、IH=IJの二等辺三角形です。
したがって、(2)からIF=IJとなります …(4)
三角形EIFと三角形GIJは合同です(IF=IJ、角EIF=角GIJ(対頂角)、角EFI=角GJIより「1辺とその両端の角がそれぞれ等しい」)。 …(★)
よって、EI=GI …(5)
台形EFGHの面積は、台形EIGHと三角形EFIの面積の和ですが、(★)より、台形EIGHと三角形GIJの面積の和、つまり二等辺三角形EJHの面積に等しいですね。
また、(4)(5)から、FG=IF+IG=IH+IJ=EJです。
準備しておいた図から、台形EFGHと面積が同じ三角形EJHの3辺の長さの関係は、上の右の方の図の通りです。
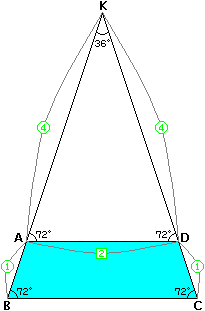
次に、台形ABCDを考えてみましょう。
BAとCD、それぞれの延長線の交点をKとします。
台形ABCDの面積は、三角形BKCから三角形AKDを取り除いたものです。
さて、三角形AKDと三角形BKCは三角形EJHと相似です(上のように角度を記入してみればわかります)。
三角形EJHと三角形AKDの相似比は、EH:AD=1:2。 …(6)
三角形AKDと三角形BKCの相似比は、EJの長さを2としたとき、(6)よりAK=2×2=4だからBK=5と表せるので、AK:BK=4:5。 …(7)
(6)(7)をまとめると、3つの三角形の相似比は、
(三角形EJH):(三角形AKD):(三角形BKC)=2:4:5
となりますから、面積比は、
(三角形EJH):(三角形AKD):(三角形BKC)=2×2:4×4:5×5=4:16:25
となります。
あとは計算だけです。
面積比 (台形ABCD):(台形EFGH)
=(三角形BKC)−(三角形AKD):(三角形EJH)
=25−16:4
=9:4
正解;9:4 |