問１２の解答

問題に戻る

＜解説＞

この問題のテーマは『折れ線の最短距離』と『正六角形の分割』です。

まずは、「三角形ＡＰＱのまわりの長さが最も短くなるように点Ｐ，Ｑをとり方」を考えます。
これは要するに、“長さの和　ＡＰ＋ＰＱ＋ＱＡ　の最小値”を考えればいいのですが…

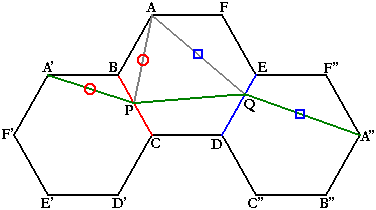
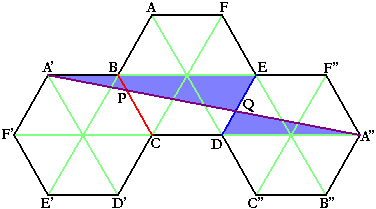
正六角形ＡＢＣＤＥＦを、辺ＢＣを折り目として折り返した正六角形をＡ'Ｆ'Ｅ'Ｄ'ＣＢ、辺ＤＥを折り目として折り返した正六角形をＥＤＣ''Ｂ''Ａ''Ｆ''とします。　
すると、明らかにＡＰ＝Ａ'Ｐ、ＡＱ＝ＱＡ''ですね。
よって、「長さの和ＡＰ＋ＰＱ＋ＱＡ」は、「長さの和ＡＰ'＋ＰＱ＋ＱＡ''」と同じです。
つまり、「長さの和　ＡＰ＋ＰＱ＋ＱＡ　の最小値」は、「長さの和　ＡＰ'＋ＰＱ＋ＱＡ''　の最小値」、つまり『点Ａ'から点Ａ''までの最短距離』を考えればいいわけです。

２点間の最短距離は直線ですから、下図のように２点Ａ'とＡ''を直線で結べば、それが最短距離となります。
このとき、ＰとＱの位置はともに判明します。

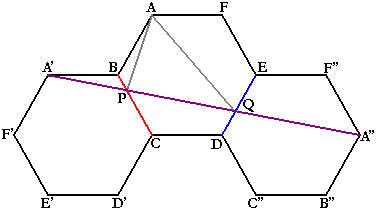
いよいよ本題（ＢＰ：ＰＣとＤＱ：ＱＥを求める）ですが、これは相似を発見することで解決しましょう。
ところが、上の図を見ても直接には相似な三角形は見つかりません。
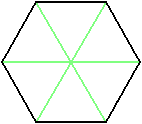
そこで、正六角形を、下のように正三角形６個に分割して考えてみましょう。
正六角形の１辺の長さを１とすると、分割された６個の正三角形の１辺の長さもすべて１となります。

（１）
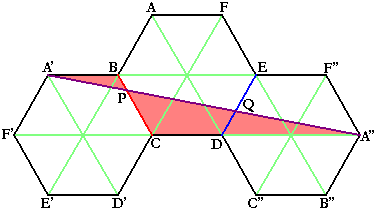
下の図において、Ａ'ＢとＣＡ''は平行なので、三角形Ａ'ＢＰと三角形Ａ''ＣＰは相似です。
相似比は、Ａ'Ｂ：Ａ''Ｃ＝１：３＝ＢＰ：ＣＰ
よって、ＢＰ：ＰＣ＝１：３となります。

（２）
さっきと同様に、三角形Ａ'ＥＱと三角形Ａ''ＤＱは相似です。
相似比は、Ａ'Ｅ：Ａ''Ｄ＝３：２＝ＥＱ：ＤＱ
よって、ＤＱ：ＱＥ＝２：３となります。

問題に戻る