問２０の解答

問題に戻る

＜解説＞

引っかけの要素が複数組み込まれた「いぢわる問題」です。
常識から抜け出さない限り、正しい答えを得ることはまず不可能でしょう。

さて、まずは展開図を普通に組み立ててみましょう。
すると、次のような立体が出来ます。

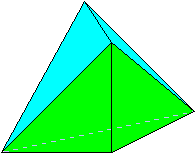
この立体は、
[Ａ]正四面体
[Ｂ]合同な３つの面が直角二等辺三角形からなる正三角すい　
からなっています。　…（★）
さて、この立体は次のように立方体から切り出すことが出来ます。

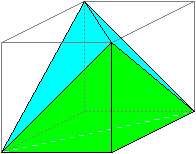
１辺の長さがＸcmの正方形から、（★）の[Ｂ]の立体３つを切り出せばいいですね。
[Ｂ]の立体の体積は、Ｘ×Ｘ÷２×Ｘ÷３＝Ｘ×Ｘ×Ｘ／６ですから、
従って、立体の体積は、Ｘ×Ｘ×Ｘ−３×Ｘ×Ｘ×Ｘ／６＝Ｘ×Ｘ×Ｘ／２です。

というわけで、Ｘ×Ｘ×Ｘ／２が４００cm²より大きく、５００cm³より小さくなる…つまり、Ｘ×Ｘ×Ｘが８００cm³より大きく、１０００cm³より小さくなるようなＸを発見すればいいわけです。ところが……

• Ｘが８以下のときは体積が小さすぎて不可
• ９×９×９＝７２９（８００より小さいので、不可）
• １０×１０×１０＝１０００（１０００より小さくないので不可）　←「１０００より小さい」には、１０００は含まれません
• Ｘをこれ以上大きくしてももちろん不可

となって、体積の条件を満たすようなＸは見つかりません。
ということは、この問題の答えは『解なし』なのでしょうか？

いえ、ちょっと待ってください。
この展開図の組み立て方は、実はもうひとつ作り方があるのです！
少々気付きにくいかもしれませんが、次のようなへこみのある立体も作ることができます。
下の図ではかなり無理のある置き方をしていますが、これは体積を求める図の都合です。

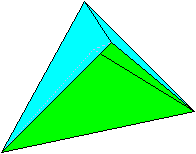
この立体は、（★）の[Ａ]から[Ｂ]を取り除いた形になっています。
この立体は、前の立体から[Ｂ]をさらに２つ切り取ったものなので、１辺の長さがＸcmの正方形から、（★）の[Ｂ]の立体５つを切り出せば完成です。

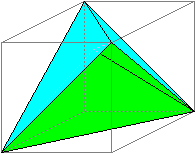
立体の体積は、Ｘ×Ｘ×Ｘ−５×Ｘ×Ｘ×Ｘ／６＝Ｘ×Ｘ×Ｘ／６です。

よって、Ｘ×Ｘ×Ｘ／６が４００cm³より大きく、５００cm³より小さくなる…つまり、Ｘ×Ｘ×Ｘが２４００cm³より大きく、３０００cm³より小さくなるようなＸを発見すればいいわけです。

• Ｘが１２以下のときは体積が小さすぎて不可
• １３×１３×１３＝２１９７（２４００より小さいので、不可）
• １４×１４×１４＝２７４４（これは体積の条件を満たしますね！）
• １５×１５×１５＝３３７５（３０００より大きいので、不可）
• Ｘをこれ以上大きくしてももちろん不可

よって、Ｘ＝１４のときのみＯＫで、その時の立体の体積は、１４×１４×１４／６＝１３７２／３cm³となります。

問題に戻る