![]() 問23の解答
問23の解答
<解説>
いくつか方法が考えられますが、いずれも「円内部の交点の数」がポイントとなるでしょう。
まず、操作後に線分が最大になるときはどういうときかを考えます…が、直感でもわかるでしょう。
円の内部に引かれる3本の直線を取り出して考えてみます。
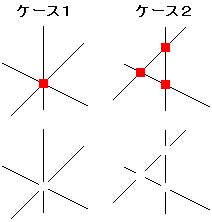
3本の直線が1点で交わるときと、そうでないときの図を描いてみました。
この2つのケースを比べると、交点を消しゴムで消すとどちらの方が線分が多くなるかは…見てのとおりわかりますよね!(^^;
というわけで、円の内部では、どの3つの直線も1点で交わらない(つまり、どの交点でも交わっている直線は2本だけの)ときに、線分の数は一番多くなります。
(円周上では、後で述べるように10本の直線が交わる場所があるので、“円の内部では”という断り書きがないと厳密にはマズイわけです)
というわけで、本題。
突然ですが、次のような約束をしておきます。
・線分の両端には●印をつける
・円周上の点には◆印をつける
・円の内部の交点には■印をつける
線分1本につき●は2つつきますから、●の数の半分が求めたい数となります。
方針としては、「◆を全部消したときにできる●の数を求める」→「■を全部消したときにできる●の数を求める」と考えてみます。
[その1]〜◆(円周上の点)を消しゴムで消す。〜
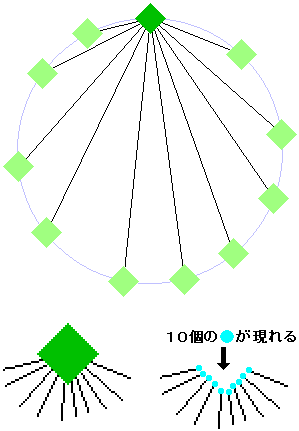
◆の1つに注目すると、ここから他の円周上の点10個に線を引くことになります。
この◆を消しゴムで消すと、線分の端が10個できます。
他の◆でも同じことがいえるので、◆を全部消すと、●は
10×11=110個現れます。
[その2]〜■(円の内部の交点)を消しゴムで消す。〜
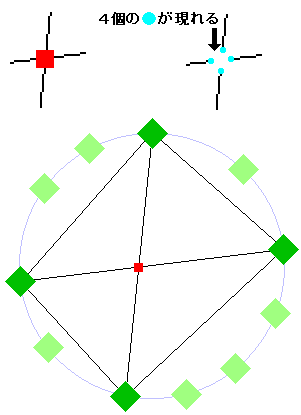
どの交点でも交わっている直線は2本だけですから、■を1つ消しゴムで消すと、線分の端が4個できます。
あとは、円の内部にできた交点の数を数えれば解決ですが…なかなか難しいですね。
ここで、4つの◆を適当に選んで結べるだけ線を引いてみてください。
すると、円の内部に交点が1個だけできましたよね!
これはつまり、交点の数は、11個の◆から4個を選ぶ場合の数と同じなんですね。
というわけで、■は11×10×9×8÷(4×3×2×1)=330個あるので、●は
330×4=1320個現れます。
以上より、●は110+1320=1430個あるので、線分はこの半分の715本あります。
| 正解;715本 |