![]() 問26の解答
問26の解答
<解説>
相当な難問です。
前半の「明らかに条件を満たす整数捜索」はともかく、後半の「それ以外の整数は条件を満たさないことの証明」はコロンブスの卵的発想?
しかし、前半も後半も当たり前な事柄が決め手となります。
まず、「各位の数字がすべて同じ整数」は、
『11..11×● (●は1以上9以下の整数)』
と表すことができます。
さてとりあえず「11..11(各位がすべて1である整数)」に注目してみましょう。
有名な倍数判定法で次のようなものがありましたね。
・2の倍数判定…1の位が0か2か4か6か8ならばその整数は2の倍数である。
・5の倍数判定…1の位が0か5ならばその整数は5の倍数である。
逆にいえば、この条件を満たさない整数は2の倍数や5の倍数ではないわけです。
「11..11」の1の位は絶対に1ですから、「11..11」は2の倍数でも5の倍数でもありません。
ここで『11..11×●』に戻り、条件を満たすような整数を見つけていきましょう。
[1]『11..11×●』が2の倍数だが5の倍数ではないとき
●=8(=2×2×2)とすると、『11..11×●』は8の倍数となります。(8の倍数は2の倍数や4の倍数を含んでいます)
しかし、2×2×2×2=16の倍数というのはできません。(「11..11」が2の倍数でないので、●=16(以上)でなければいけなくなります)
というわけで、□が16の倍数のとき、条件を満たします。
[2]『11..11×●』が5の倍数だが2の倍数ではないとき
●=5とすると『11..11×●』は5の倍数となります。
しかし、5×5=25の倍数というのはできません。(「11..11」が5の倍数でないので、●=25(以上)でなければいけなくなります)
というわけで、□が25の倍数のとき、条件を満たします。
[3]『11..11×●』が2の倍数だが5の倍数のとき
「11..11」が2や5の倍数でないので、●=10(以上)でなければいけなくなりますが、●は1以上9以下なのでそれを満たすような●はありません。
というわけで、□が10の倍数のとき、条件を満たします。
ここまでで、□が16の倍数か25の倍数か10の倍数であれば、条件を満たすことがわかりました。
1以上1000以下の整数で、条件を満たす整数の個数を求めましょう。
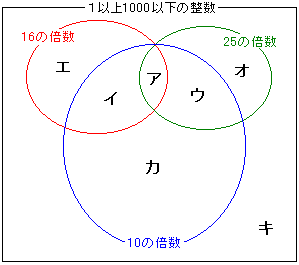
地道に数えていくこともできますが、ここではベン図を使って考えてみましょう。
1000÷16=62あまり8→62個=ア+イ+エ
1000÷25=40個=ア+ウ+オ
1000÷10=100個=ア+イ+ウ+カ
1000÷400=2あまり200 →2個 =ア (400は、16と25と10の最小公倍数)
1000÷80=12あまり40→12個=ア+イ(80は16と10の最小公倍数)より、12−2=10個=イ 62−12=50個=エ
1000÷50=20個=ア+ウ(50は25と10の最小公倍数) より、20−2=18個=ウ、40−20=20個=オ
求めたい個数は(ア+イ+ウ+カ)+エ+オ=100+50+20=170個です。
これで正解は170個…といきたいところですが、ここまでで厳密に議論できたのは16の倍数と25の倍数と10の倍数のみです。
□がそれ以外のときはどのように考えたらいいのでしょうか?
実は、2の倍数や5の倍数以外ならどんな整数の倍数の中にも「11..11」という形のものが存在しているのです!
それを証明してみましょう。
2の倍数でも5の倍数でもない整数★を用意し、(★+1)個の整数
1,11,111,…,11..(1が★+1個並ぶ)..11を次々と★で割っていきます。
すると、余りが同じになるようなものが必ず出てきます。
ここで「何故?」と思ってしまうかもしれないのですが、言われてみれば「なーんだ」と思うことでしょう。
★で割った余りというのは何通り考えられるでしょうか? 0,1,2,…,(★−1)の★通りですよね。
しかし、ここでは(★+1)個の異なる整数を★で割りました。★通りのあまりを(★+1)個の整数に全部異なるように振り分けることは…もちろん不可能ですから、必ず余りが同じモノが出てきてしまいます。
次に、★で割った余りが同じである2数の差は、★の倍数であることを考えます。
このような2数を引くとあまりは消えちゃいますし、★の倍数から★の倍数を引くともちろん★の倍数ですから、これは簡単に説明がつきます。
さて、この2数の差を筆算で書いてみると、
11..1111..11 − 11..11 ----------------------- 11..1100..00
となりますから、11..1100..00が★の倍数になるわけです。
ところで、11..1100..00=11..11×100..00と表すことができます。
★は2の倍数でも5の倍数でもないと仮定しましたから、100..00と★は互いに素(最大公約数は1)です。
このことから、★は11..11で割りきれなければならないことがわかりました。
つまり、2の倍数でも5の倍数でもない整数★の倍数の中には11..11で表されるものの存在が示されました。
というわけで、□が16の倍数か25の倍数か10の倍数の場合のみ条件を満たし、その個数は170個です。
| 正解;170個 |