問２７の解答

問題に戻る

＜解説＞

まずは展開図を組み立ててみると、問題文にもあるように、三角すいになります。
三角すいの頂点に、次のように勝手に記号をつけました。
※以下の画像にある数字の単位は、すべて cm です。

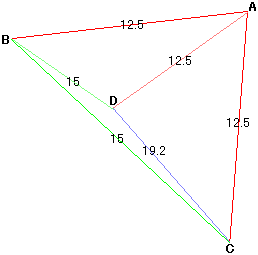
このままでは、どの面を底面にしても、高さを求めるのは厄介です。
そこで、この立体を切断してみることにします。

切断する前に、面ＡＢＣについて調べてみます。
一目でＡＢ＝ＡＣの二等辺三角形、ということがわかりますが、それだけではなくこの三角形は特殊な図形です。
ＡからＢＣに向けて垂線を引き、その足をＭとします。　このとき点ＭはＢＣの中点（真ん中の点）なのでＢＭ＝１５÷２＝７.５cmです。

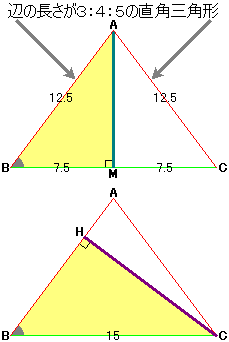
三角形ＡＢＭにおいて、角ＡＭＢ＝９０度、ＡＢ：ＢＭ＝１２.５：７.５＝５：３です。
このことから、三角形ＡＢＭは、辺の長さの比が３：４：５の直角三角形であることがわかります。（ＡＢ：ＡＭ：ＢＭ＝５：４：３ですね）

次に、ＣからＡＢに向けて垂線を引き、その足をＨとします。
このときできた三角形ＣＢＨは、三角形ＡＢＭと相似です。
（角ＣＢＨ＝角ＡＢＭは共通、角ＡＭＢ＝角ＣＨＢ＝９０度より、２組の角がそれぞれ等しいから）
よって、ＣＢ：ＣＨ＝１５：ＣＨ＝ＡＢ：ＡＭ＝５：４なので、ＣＨ＝１５×４÷５＝１２cmです。

さて切断の話に戻りましょう。
三角すいを、３点Ｃ・Ｄ・Ｈを通る平面で切断します。

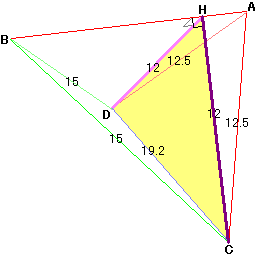
三角すいＡ−ＨＤＣとＢ−ＨＤＣの体積の和を求めることになりますが、両方とも面ＨＤＣを底面と見ると、高さはそれぞれＡＨとＢＨにあたります。
したがって体積は、（底面積）×ＡＨ÷３＋（底面積）×ＢＨ÷３
＝（底面積）×（ＡＨ＋ＢＨ）÷３＝（底面積）×１２.５÷３　となり、あとは三角形ＨＤＣの面積を求めるだけです。

その三角形ＨＤＣですが、これもまた特殊な二等辺三角形なのです。

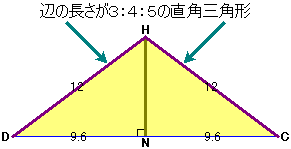
ＨからＢＣに向けて垂線を下ろし、その足をＮとします。　ＮはＤＣの中点で、ＤＮ＝１９.２÷２＝９.６cmです。
三角形ＨＤＮにおいて、角ＨＮＢ＝９０度、ＨＤ：ＤＮ＝１２：９.６＝５：４です。
このことから、三角形ＨＤＮは、辺の長さの比が３：４：５の直角三角形であることがわかります。（ＨＤ：ＤＮ：ＨＮ＝５：４：３ですね）
よって、ＨＮ＝１２×３／５＝７.２cmとわかります。
ゆえに、三角形ＨＤＮの面積は、１９.２×７.２÷２で求まります。

求めたい三角すいの体積は、１９.２×７.２÷２×１２.５÷３＝２８８cm³です。

問題に戻る