問３２の解答

問題に戻る

＜解説＞

解き方自体は有名な「正四角すいの切断問題」と大差ありませんが、視点を何度も変える必要があるので意外に手を焼く問題かもしれません。

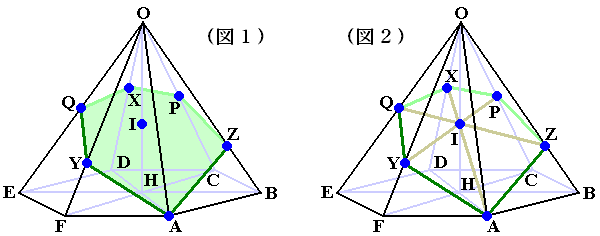
ここで、「三角すいの体積比を求める定理(★)」を思い出す必要があります。
有名な定理ですが、知らない方は以下をご覧ください。

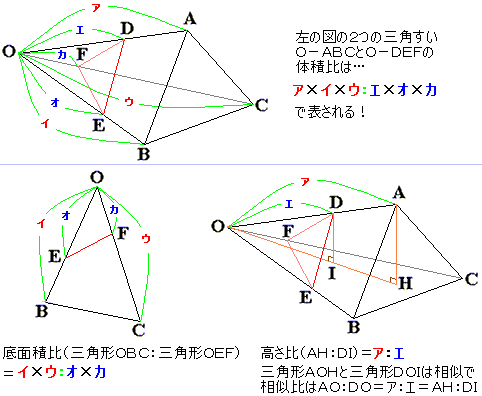
さて、△ＯＤＡが真正面にくるように正六角すいを見たのが、図３です。
この方向から見ると、対称性より切断面は直線に見えることになります。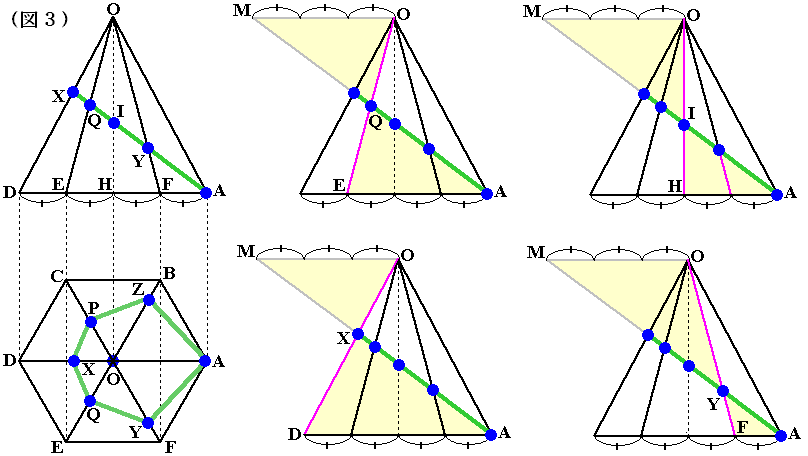

Ｏを通り、ＡＤと平行な線を引き、切断面の延長との交点をＭとします。
すると、△ＱＥＡと△ＱＯＭはチョウチョ型相似で、相似比ＱＥ：ＱＯ＝１：１…つまり合同な三角形です。
よって、ＤＥ＝１メモリとすれば、ＥＡ＝３メモリだからＯＭも３メモリです。
以下、メモリに着目することにより、長さの比が芋ヅル式に求まります。
　△ＸＤＡと△ＸＯＭは相似で、相似比ＤＡ：ＯＭ＝４：３＝ＤＸ：ＯＸ …ア
　△ＩＨＡと△ＩＯＭは相似で、相似比ＨＡ：ＯＭ＝２：３＝ＨＩ：ＯＩ …イ
　△ＹＦＡと△ＹＯＭは相似で、相似比ＦＡ：ＯＭ＝１：３＝ＦＹ：ＯＹ …ウ

なお、対称性より明らかに ＢＺ：ＯＺ＝ＦＹ：ＯＹ＝１：３ が成立します。

辺の長さをまとめます。　ＯＡ＝ＯＢ＝ＯＣ＝ＯＤ＝ＯＥ＝ＯＦ＝１とすると、
題意よりＯＰ＝ＯＱ＝１／２、 アよりＯＤ＝３／７、 イよりＯＩ＝３／５、 ウよりＯＹ＝ＯＺ＝３／４
となります。

では体積比を求めます。定理★と図４を参考にしてください。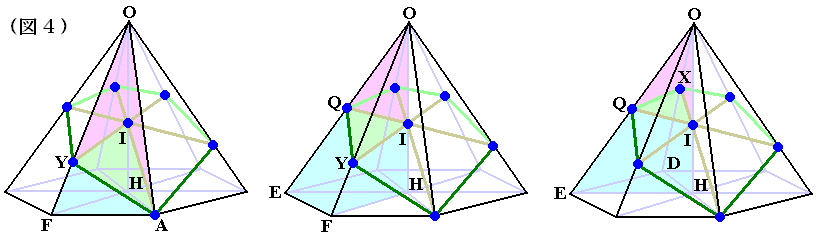

Ｏ-ＨＦＡ：Ｏ-ＩＹＡ＝１×１×１ ： ３／５×３／４×１ ＝ １：９／２０ (Ｏ-ＨＡＢ：Ｏ-ＩＡＺも同様)
Ｏ-ＨＥＦ：Ｏ-ＩＱＹ＝１×１×１ ： ３／５×１／２×３／４ ＝ １：９／４０ (Ｏ-ＨＢＣ：Ｏ-ＩＺＰも同様)
Ｏ-ＨＤＥ：Ｏ-ＩＸＱ＝１×１×１ ： ３／５×３／７×１／２ ＝ １：９／７０(Ｏ-ＨＣＤ：Ｏ-ＩＰＸも同様)

というわけで、正六角すいと切断面より上の立体の体積比は、
(Ｏ-ＨＡＢ＋Ｏ-ＨＢＣ＋Ｏ-ＨＣＤ＋Ｏ-ＨＤＥ＋Ｏ-ＨＥＦ＋Ｏ-ＨＦＡ)：(Ｏ-ＩＡＺ＋Ｏ-ＩＺＰ＋Ｏ-ＩＰＸ＋Ｏ-ＩＸＱ＋Ｏ-ＩＱＹ＋Ｏ-ＩＹＡ)
＝１×６：(９／２０＋９／４０＋９／７０)×２＝６：４５／２８＝５６：１５
（Ｏを含むほうの立体）：（Ｏを含まないほうの立体）＝１５：(５６−１５)＝１５：４１　が正解となります。

問題に戻る