問３３の解答問３３の解答
＜解説＞
図はシンプルですが、意外に難しい問題です。 あることに気がつくかどうか…
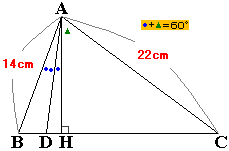まずは、角ＨＡＣ＝▲とします。すると、問題文より●＋▲＝６０度となります。
さて、ここで６０度を３倍すれば１８０度、つまり一直線になります。
３×（●＋▲）＝３×６０＝１８０度なので、●が３個分、▲も３個あれば一直線を作れますが、●３個と▲１個はすでに図にあります。
ということで、あとは▲２個あれば一直線のできあがりですね。
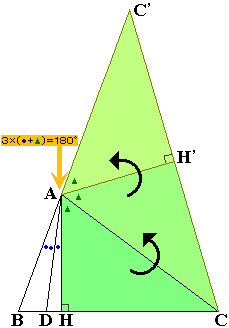ここで右図をご覧ください。
三角形ＡＨＣを、ＡＣを軸にして折り返して三角形ＡＨ'Ｃを作り、さらに三角形ＡＨ'ＣをＡＨ'を軸にして折り返して三角形ＡＨ'Ｃ'を作ったところです。
すると、頂点Ａには●が３個、▲も３個集まるので、３点Ｂ・Ａ・Ｃ'は一直線上にあることになります。
しかも、３点Ｃ'、Ｈ'、Ｃも一直線上にあります。（その理由は明らかですね）
つまり、巨大な三角形Ｃ'ＢＣが完成したというわけです。
このことに気付けば、あとは簡単です！
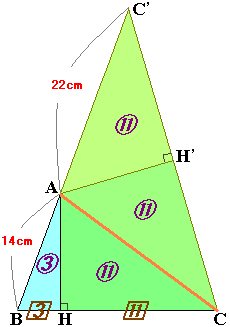三角形ＡＨＣの面積を１１としてみます。すると当然三角形ＡＨ'Ｃと三角形ＡＨ'Ｃ'の面積も１１ですね。
三角形Ｃ'ＡＣと三角形ＡＢＣの面積比はＣ'Ａ：ＡＢ＝２２：１４です。（「線分比と面積比」の考えによる）
三角形ＣＡＣ'の面積は、１１×２＝２２と表されるので、三角形ＡＢＣの面積は１４となります。
三角形ＡＢＨの面積は、三角形ＡＢＣから三角形ＡＨＣを引けば１４−１１＝３となります。
三角形ＡＢＨと三角形ＡＨＣは、それぞれＢＨとＨＣを高さと見ると、高さはともにＡＨとなるので、「線分比と面積比」の考えにより、（三角形ＡＢＨの面積）：（三角形ＡＨＣの面積）＝３：１１＝ＢＨ：ＨＣとわかるのです。
| 正解；３：１１ |