![]() 問35の解答
問35の解答
<解説>
例によって、枚数を少なくして規則を見つけるのが方針ですが、見慣れない規則のため苦労させられるでしょう。
まずは、カードの並べ方をわかりやすく「視覚化」することにしましょう。
カードの隣に来ることができる数を線で結ぶことにすると、12枚カードを並べる場合は、次のようになります。
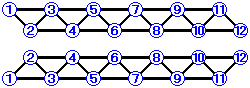
こうすると、カードの並べ方を「同じ道は通らずにすべての番号を通る道順の問題」としてとらえることができますね。
もちろん、上下どちらの表し方でもいいわけですが、特に断りのない限り上の表記で統一することにします。
でもいきなり12枚の場合で考えるのは大変ですから、カードの枚数をもっと少なくして“実験”してみることにします。
実験することによって、何らかの規則を発見する、という狙いです。
・カードが1枚…当然1通り。
・カードが2枚…1→2 の1通り。
・カードが3枚…1→2→3 1→3→2 の2通り。
・カードが4枚…1→2→3→4 1→2→4→3 1→3→2→4 1→3→4→2 の4通り。
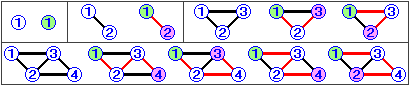
…まったく規則は見えてきませんね。
では、カードが5枚の場合を詳しく調べてみると…
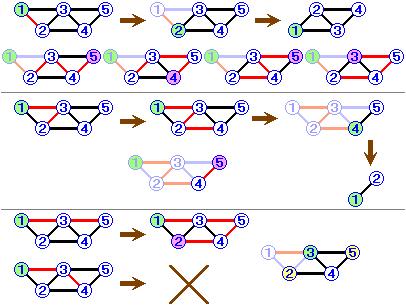
・1→2 の順に通るとき。
残りの道を取り出すと、実はカードを4枚並べるとき(=カードを1枚少なくしたとき)とまったく同じ状況になります。
2〜5のカードの数字をそのまま1〜4に置きかえればいいわけです(図2の、カードが4枚の図とはちょっと違いますが、上下が逆なだけで本質的には同じですね)。
よって、4通り(1→2→3→4→5 1→2→3→5→4 1→2→4→3→5 1→2→4→5→3)の通り方があります。
・1→3→2 の順に通るとき。
次は4に進むしかありません。
残りの道を取り出すと、今度はカードを2枚並べるとき(=カードを3枚少なくしたとき)とまったく同じ状況です。
よって、このケースでは1通り(1→3→2→4→5)の通り方があります。
・それ以外の通り方のとき。
1→3→5 の順に通ると、1→3→5→4→2 の順に進むしかなく、1通りとなります。
1→3→4 の順に通ると、右上の番号と左下の番号のどちらかが通れなくなるので手詰まり。
(つまり、それ以外の通り方をするには、右上の番号と左下の番号の両方を通るために、ずっと右に進み上段の奇数をすべて通ってから下段に下りてずっと左に進みすべての偶数を通る1通りしかないのです) …(★)
以上から、
(カードが5枚の並べ方)=(カードが4枚の並べ方)+(カードが2枚の並べ方)+1=4+1+1=6通り と表せるわけです。
この考えは、カードが6枚以上のときにも使えます。
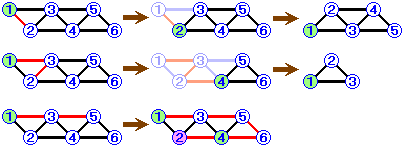
・1→2の順に通るときは、残りの道を取り出すと、カードを(1枚少なくした)5枚並べるときとまったく同じ状況。
・1→3→2の順に通るときは、4まで進んだ残りの道を取り出すと、カードを(3枚少なくした)3枚並べるときとまったく同じ状況。
・それ以外の通り方としては、(★)の通り方、つまり 1→3→5→6→4→2 しかありません。
よって、(カードが6枚の並べ方)=(カードが5枚の並べ方)+(カードが3枚の並べ方)+1=6+2+1=9通り です。
これで規則がわかりましたね! あとは計算していくだけです。
(カードが7枚の並べ方)=(カードが6枚の並べ方)+(カードが4枚の並べ方)+1=9+4+1=14通り
以下同様に、
(カードが8枚の並べ方)=14+6+1=21通り
(カードが9枚の並べ方)=21+9+1=31通り
(カードが10枚の並べ方)=31+14+1=46通り
(カードが11枚の並べ方)=46+21+1=68通り
(カードが12枚の並べ方)=68+31+1=100通り
よって、答えは100通り、となります。
| 正解;100通り |