問37の解答

問題に戻る

＜解説＞
平面図形の扱いに慣れている人にとってはさほど難しくは感じないかもしれませんが、実際は文句なく難問です。

まず、三角形ＡＢＰを、点Ａを中心として、ＡＢがＡＣと重なるように回転移動させます。
移動後の点ＰをＰ'と名付けます。
（ありゃ、図が巨大過ぎるかも...まいっか(^^;）

ＡＰ＝ＡＰ'であることに注意すると、三角形ＡＢＣと三角形ＡＰＰ'は「２辺と長さの比と、その間の角が等しい」ので相似ですね（この相似判定法は高度ですが、小学生であれば感覚的に「頂角の等しい二等辺三角形は相似」でも十分でしょう）
相似比はＡＢ：ＡＰ'＝１４：１０＝７：５　ですから、面積比は７×７：５×５＝４９：２５です。
従って、面積比…三角形ＡＢＣ：三角形ＡＰＰ'：四角形ＰＢＣＰ'＝４９：２５：４９−２５＝４９：２５：２４です。　…（☆）

次に、角ＰＢＣ＝●、角ＢＣＰ＝▲、角ＣＰＢ＝■として、図に角度を記入していきます。
角ＰＢＣ＝角ＡＣＰであることに注意すると、下の左図のようになります。
ここで●＋▲＋■＝１８０度（三角形ＰＢＣの内角の和）に注目します。
左図の角ＰＣＰ'には●と▲が集まっています。　この部分に、あと■が集まれば一直線ができますね。
そこで、三角形ＰＢＣを、ＰがＣに、ＣがＰに重なるようにひっくり返してみます。
移動後の点ＢをＢ'と名付けます。

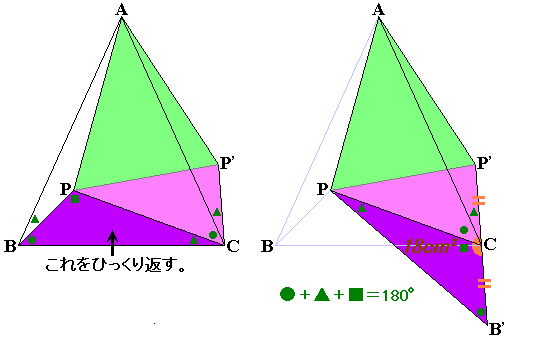
すると上の右図のようになり、頂点Ｃには●と▲と■が集まり、３点Ｐ'・Ｃ・Ｂ'は一直線上にあることがわかります。
よって、面積比…三角形ＰＢ'Ｃ：三角形ＰＣＰ'＝Ｂ'Ｃ：ＣＰ'です。
しかし、Ｂ'Ｃ＝ＣＰ'（どちらも辺ＰＢを移動したもの）ですから、結局三角形ＰＢ'Ｃと三角形ＰＣＰ'の面積は等しいですね！

四角形ＰＢＣＰ'の面積は、三角形ＰＢＣの面積の２倍で３６cm²です。
（☆）より、三角形ＡＢＣの面積は、　３６×４９／２４＝７３.５cm²です。

問題に戻る