問43の解答
問題に戻る
＜解説＞
高さを１０cmずつ増やしていき、最上部の積み方に注目すると…。
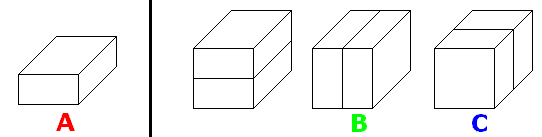高さが１０cmのとき、明らかに１通りです。
このブロックの置き方を『Ａ』とします。
高さが２０cmのとき、右上図のように３通りです。
図のようなブロックの置き方をそれぞれ『Ｂ』『Ｃ』とします。
では高さが３０cmの場合はどうでしょうか。
一番上の積み方が、『Ａ』か『Ｂ』か『Ｃ』の積み方に限られることに着目します。
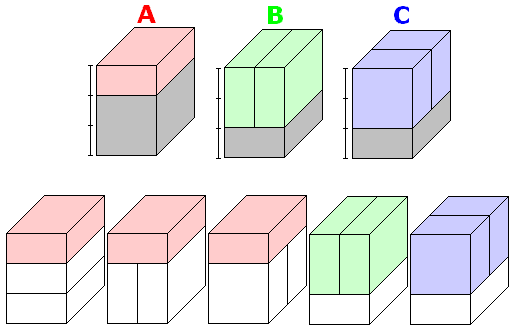・一番上が『Ａ』の積み方の場合
一番上のブロックを取り除いた ３０−１０＝２０cm の高さに積む方法を考えればよく、３通り。
・一番上が『Ｂ』の積み方の場合
一番上のブロックを取り除いた ３０−２０＝１０cm の高さに積む方法を考えればよく、１通り。
・一番上が『Ｃ』の積み方の場合
一番上のブロックを取り除いた ３０−２０＝１０cm の高さに積む方法を考えればよく、１通り。
以上より、３＋１＋１＝５通りです。
この要領でいけば、高さが４０cm以降も大丈夫です。
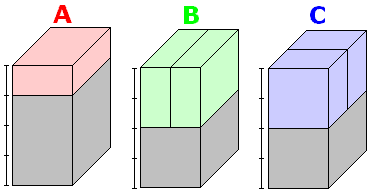・一番上が『Ａ』の積み方の場合、 ４０−１０＝３０cm の高さに積む方法を考えて、５通り。
・一番上が『Ｂ』の積み方の場合、 ４０−２０＝２０cm の高さに積む方法を考えて、３通り。
・一番上が『Ｃ』の積み方の場合、 ４０−２０＝２０cm の高さに積む方法を考えて、３通り。
以上より、５＋３＋３＝１１通りです。
ということは、高さが５０cmのときは、
（一番上が『Ａ』）＋（一番上が『Ｂ』）＋（一番上が『Ｃ』）
＝（高さ４０cmの積み方）＋（高さ３０cmの積み方）＋（高さ３０cmの積み方）
＝１１＋５＋５＝２１通りです。
以下同様にして、高さが６０cmのとき、
（高さ５０cmの積み方）＋（高さ４０cmの積み方）＋（高さ４０cmの積み方）
＝２１＋１１＋１１＝４３通り。
高さ７０cmのとき ４３＋２１＋２１＝８５通り
高さ８０cmのとき ８５＋４３＋４３＝１７１通り
高さ９０cmのとき １７１＋８５＋８５＝３４１通り
高さ１ｍのとき ３４１＋１７１＋１７１＝６８３通り
問題に戻る