![]() 問46の解答
問46の解答
<解説>
この手の立方体の穴あけ問題は「1段ずつスライスして考えよ」が定石なのですが、この問題ではそれは面倒過ぎます。
(1段スライスするだけで27×27=729個の升目が必要になってきます)
そこで、穴のあけ方の規則性に注目してみましょう。
まずは、以下の問題を考えてください。
『3×3×3=27個の小立方体を積み上げて大きな立方体を作ります。 この立体の中心に図のように穴を開け、向かい側の面までまっすぐ通します。 穴を開けた後の立体の体積は、もとの立方体の体積の何倍ですか?』
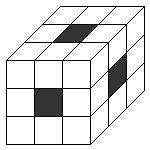
説明:取り除かれた部分は下の図のようになります。
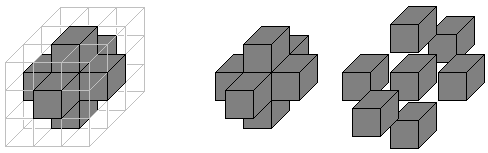
結局、小立方体が7個取り除かれたことになるんですね。
よって、体積はもとの (27−7)÷27=20/27倍。 …<★>
今回の限界編は、これを利用します。
たっくさんの穴が開いてしまってますが、穴の大きさ別に考えていきます。
まずは一番大きい穴だけを相手にします。
各面に開いた穴の大きさは、1辺が9cmの正方形の形です。
そこで、次のように9cmごとに区切り線を入れてみると…
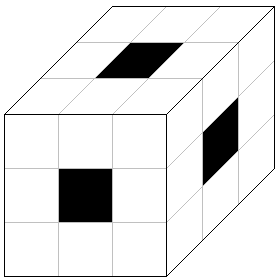
どうでしょう? さきほどの<★>の問題とまったく同じ状況であることがわかりますよね?
というわけで、一番大きい穴だけを開けると、もとの立方体の体積の20/27倍となります。 …<ア>
次に、中型の穴だけを開けます。
各面に開いた穴の大きさは、1辺が3cmの正方形の形です。
そこで、次のように3cmごとに区切り線を入れてみると…
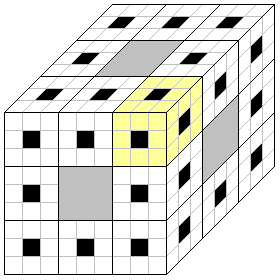
一見複雑そうに見えますが、結局薄く色付けした立体が集まったもの、と考えることができます。
色付けした立体の体積は、<★>より大きなの穴を開ける前の20/27倍です。
したがって、中型の穴を開けると、<ア>の時と比べて更に20/27倍となります。
つまり、もとの立方体の体積の(20/27)×(20/27)倍ですね。 …<イ>
最後に、一番小さな穴を開けてみます。
各面に開いた穴の大きさは、1辺が1cmの正方形の形です。
そこで、次のように1cmごとに区切り線を入れてみると…
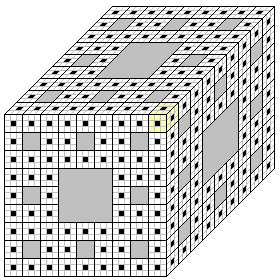
もう予想はできると思いますが、さっきと同じく、やっぱり薄く色付けした立体が集まったものなんですね。
色付けした立体の体積は、<★>より中型の穴を開ける前の20/27倍です。
したがって、小型の穴を開けると、<イ>の時と比べて更に20/27倍となります。
つまり、もとの立方体の体積の(20/27)×(20/27)×(20/27)倍ですね。 …<ウ>
というわけで、求めたい立体の体積は、
27×27×27×(20/27)×(20/27)×(20/27)=8000cm3
とわかります。
正解;8000cm3 |