![]() 問47の解答
問47の解答
<解説>
まず次のように補助線を引きます。(こんなん思いつかねえ!ていうツッコミは却下の方向で(^^;;)
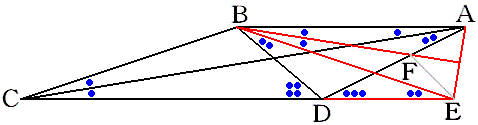
角ABDを二等分する線を引き、CDの延長線との交点をEとします。
また、角ABEを二等分する線を引き、ADとの交点をFとします。
いま、角ACD=●と表すことにすると、問題文より、
角CAD=●●、角BDC=●●●●と表せます。
以下、ABとCDが平行なことなどを考慮すると、図のように角度の大きさがわかります。
次に、△DABと△DBFは、2組の角度の大きさが等しい(角DAB=角DBF、角ADB=角BDF)ので相似です。
したがって、比例式 DA:DB=DB:DF が成立します。 …★
ここで、△DBEは角DBE=角DEBより、DB=DEです。
これをさきほどの比例式★にあてはめると、
DA:DE=DE:DF となります。 …☆
この式をもとに、△DEAと△DFEに注目します。
この2つの三角形は、☆より2組の辺の比が等しく、さらにその間の角(角ADEと角EDF)も共通なので等しいです。
したがって、△DEAと△DFEは相似な三角形であることがわかります。
したがって、角DAE=角DEFです。 …(A)
ところで、△ABCは、角BCA=BACよりBC=BAです。
そして、△BCEは、角BCE=角BECよりBC=BEです。
このことから△BEAは、BE=BAの二等辺三角形であることがわかります。
さあ、答えまでもう一息です。
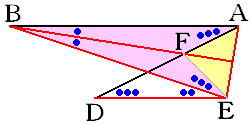
△BEFと△BAFにおいて、
BE=BA、BF共通、角EBF=角ABFより、2辺とその間の角が等しいので合同。
よって角BEF=角BAF=●●●です。 …(B)
また、FE=FAより△FEAは角FEA=角FAEの二等辺三角形です。 …(C)
(A)(B)(C)より、角DEF=●●●●●=角FAE=角FEA。
また、△FDEにおいて三角形の外角の性質を使うと、角EFA=●●●●●●●●。
以上より、△FEAの内角はすべて●を使って表すことができ、
●(5+5+8=)18個分が180度になりますから、●=10度。
(1)内角A=10×3=30度
(2)内角B=180−10×2=160度
正解;(1)30° (2)160° |