問49の解答問49の解答
＜解説＞
どの点を通れば良いのかにこだわるよりも、まずは切断面の形から決めていった方がミスを防げるでしょう。
＜本解＞
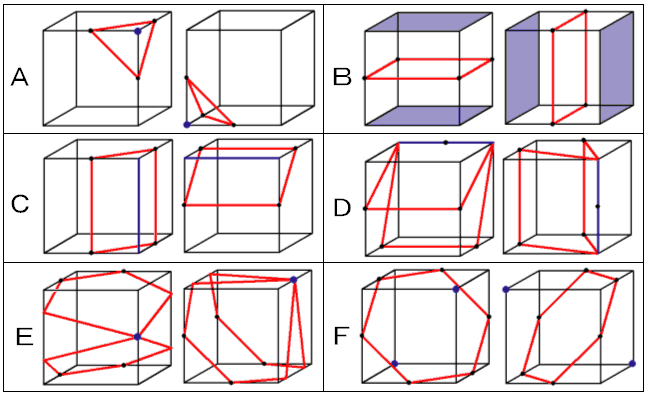Ａ：正三角形
立方体の頂点１個と対応させることができるので、頂点の個数と同じ８通り
Ｂ：正方形
互いに平行な２面に対応させることができます。面は６つあるので６÷２＝３通り
Ｃ：長方形（細長い）
立方体の辺１本に対応させることができますから、辺の本数と同じ１２通り
Ｄ：長方形（正方形に近い）
立方体の辺１本あたり２つの長方形を作れるので２×１２＝２４通り
Ｅ：五角形
中点１個あたり２つの五角形を作れます。中点は１２個あるので２×１２＝２４通り
Ｆ：正六角形
立方体の向かい合う頂点２個と対応させることができるので、８÷２＝４通り
以上より ８＋３＋１２＋２４＋２４＋４＝７５通り です。
＜別解＞
少し高度ですが、重複度に着目した解き方もあるようです。
一般に、同一直線上にない３点を選べば、切断面がただ１通りに決まります。
立方体の中点１２個から３点を選ぶ方法は12Ｃ3＝２２０通り
ただし、この中には「立方体を切断しない場合」「３点より多くの点が同一平面上に並ぶ場合」があるので、そのぶんを引く必要があります。
あ：立方体を切断しないもの
立方体の同一面上にある４点を選んでも立方体は切断しませんから、これらを丸々除きます。
4Ｃ3＝４通り：１面あたり ４×６＝２４通り
い：４点が同一平面上にある切断面
上の解説におけるＢとＣの切断です。切断面の４点から３点を選ぶ方法は4Ｃ3＝４通りですが、数えたいのは１つだけです。
すなわち、切断面１つにつき４−１＝３通り取り除く必要がありますから、（３＋１２）×３＝４５通り
う：６点が同一平面上にある切断面
上の解説におけるＦの切断です。切断面の６点から３点を選ぶ方法は6Ｃ3＝２０通りですが、数えたいのは１つだけです。
すなわち、切断面１つにつき２０−１＝１９通り取り除く必要がありますから、４×１９＝７６通り
以上より ２２０−（２４＋４５＋７６）＝７５通り です。
＜本解＞は丁寧に数え上げるという算数らしい解法ではあるが、ＤとＥが相当に数えにくい。
＜別解＞は数え上げが少なくて済み楽であるものの、「重複度」の考えは小学生には酷だろう。
正解；７５通り |