問50の解答
問題に戻る
＜解説＞
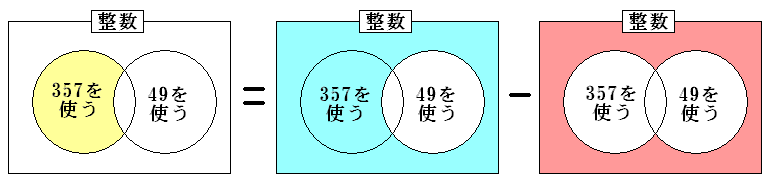
「３・５・７は使うが４・９は使わない整数」をベン図で表すと上の左図のようになります。
これは言い換えると、「４・９を使わない整数」から「３・５・７・４・９を使わない整数」を取り除いたものと考えることが出来ます。
つまり、「０１２３５６７８だけを使う整数」から「０１２６８だけを使う整数」を除いたものということです。
ここで ０，１，２，３，５，６，７，８ をそれぞれ ０，１，２，３，４，５，６，７ に置き換えれば普通の８進法になります。…★
そして ０，１，２，６，８ をそれぞれ ０，１，２，３，４ に置き換えれば普通の５進法の表記になります。…☆
『１６３２２』を普通の８進法に直せば、★より「１５３２２(8)」です。これは１０進法に直せば、
１×８×８×８×８＋５×８×８×８＋３×８×８＋２×８＋２×１＝６８６６番目の数、となります。
次に、『１６３２２』までに ０，１，２，６，８ で表される取り除くべき整数がいくつあるのかを数えます。
このような整数のうち、１６３２２以下で最大のものは、「１６２＊＊」で表されるもので最大の『１６２８８』です。
『１６２８８』を普通の５進法で表すと、☆より「１３２４４(5)」です。これを１０進法に直せば、
１×５×５×５×５＋３×５×５×５＋２×５×５＋４×５＋４×１＝１０７４番目の数、となります。
従って、６８６６番目までに、取り除くべき整数が１０７４個あるので、 ６８６６−１０７４＝５７９２番目！
問題に戻る