問54の解答

問題に戻る

＜解説＞

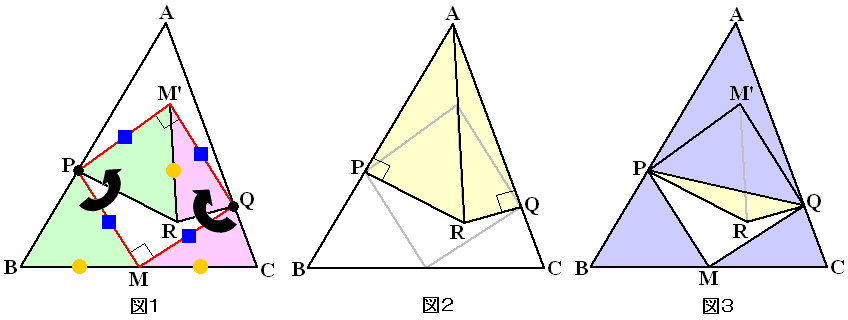
△ＰＢＭをＰを中心に反時計回りに回転、△ＱＭＣをＱを中心に時計回りに回転させます。
回転後の２つの点Ｍが重なる点をＭ'とします。（図１）
このとき、四角形Ｍ'ＰＭＱは四辺の長さが等しいのでひし形、しかも角ＰＭＱ＝９０度なので正方形です。　…（☆）
さらに角ＰＭＢ＋角ＱＭＣ＝１８０−角ＰＭＱ＝９０度なので、実は回転後の点Ｂと点Ｃも一致します。（この点をＲとする）

次に、四角形ＡＰＲＱの面積が求めます（図２）。
☆より角Ｍ'ＰＭ＝９０度ですから、角ＢＰＭ＋角ＡＰＭ'＝９０度 ＝角ＲＰＭ'＋角ＡＰＭ'＝角ＡＰＲ。
同様に考えると、角ＡＱＲ＝９０度となります。
以上から、四角形ＡＰＲＱを２つの直角三角形に分けることができ、ＰＢ＝ＰＲ＝７cm、ＱＣ＝ＱＲ＝３cmより、
９×７÷２＋１１×３÷２＝４８cm²が四角形ＡＰＲＱの面積です。　…（★）

いよいよ各部分の面積比を求めてみましょう（図３）
△ＡＢＣの面積を（９＋７）×（１１＋３）＝２２４とします
すると、△ＡＰＱ＝２２４×（９／１６）×（１１／１４）＝９９、
△ＰＢＭ＝２２４×（７／１６）×（１／２）＝４９、
△ＱＭＣ＝２２４×（３／１４）×（１／２）＝２４。
よって、直角二等辺三角形ＰＭＱ＝２２４−（９９＋４９＋２４）＝５２　＝直角二等辺三角形Ｍ'ＰＱ。
ところで、四角形Ｍ'ＰＲＱは、△ＰＢＭと△ＱＭＣを移動させてくっつけた図形ですから、４９＋２４＝７３。
よって、△ＰＲＱ＝四角形Ｍ'ＰＲＱ−△Ｍ'ＰＱ＝７３−５２＝２１。

四角形ＡＰＲＱ＝△ＡＰＱ＋△ＰＲＱですから、
面積比　△ＡＢＣ：四角形ＡＰＲＱ＝２２４：９９＋２１＝２８：１５なので、
★とあわせれば、△ＡＢＣの面積は４８×（２８／１５）＝８９.６cm²と求まるわけです。

問題に戻る