算数限界編問66の解答

問題に戻る

＜解説＞
角の二等分線があるので、とりあえず「アレ」の出番ということになりますが…その後にもう一山あります。


△ＤＰＣをＰＣについて折り返し△ＦＰＣをつくり、△ＥＢＰをＢＰについて折り返し△ＧＢＰをつくります。

すると、上の図のようになります。当然、△ＤＰＣと△ＦＰＣは合同、△ＥＢＰと△ＧＢＰは合同です。…(壱)
また、ＢＧ＝ＢＥ＝１２cm、求めたいＣＤの長さはＣＦの長さと等しくなります。
●●■■＝１８０−１２０＝６０度なので●■＝６０÷２＝３０度。△ＰＢＣの外角より、角ＥＰＢ＝角ＤＰＣ＝●■＝３０度。
角ＥＰＤ＝１８０−３０＝１５０度、角ＧＰＦ＝１８０−３０×３＝９０度です。…(弐)

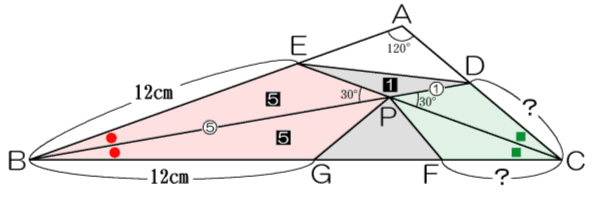
高さの等しい三角形が沢山あるので、ここからは底辺比と面積比に着目します。

△ＥＰＤの面積を[１]とすると、△ＥＢＰ：△ＥＰＤ＝５：１であることと(壱)より、△ＥＢＰ＝[５]＝△ＧＢＰ。
あとは△ＧＦＰの面積が求まれば、△ＰＢＣ：△ＰＣＤ＝ＢＰ：ＰＤ＝５：１から、何とか答えが求まりそうです。

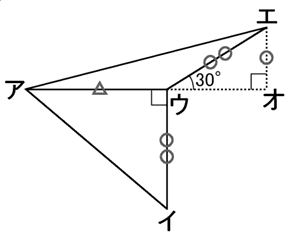右の図は、△ＧＦＰと△ＰＤＥをくっつけたものです。
折り返しよりＰＧ＝ＰＥ・ＰＦ＝ＰＤは明らかなので、辺をぴったりとくっつけられます。
なお、図では△ＰＧＦ→△アイウ・△ＰＤＥ→△ウエアとなっています。
角アウエ＝１５０度に着目すると、三角定規(△ウエオ)をつくることができます。
△ウエオは正三角形の半分で、エオの長さはウエ(＝ウイ)の長さの半分です。…(参)

面積比△アイウ：△ウエアは、底辺アウ共通、高さの比は(参)よりウイ：エオ＝２：１。
△ウエア→△ＰＤＥの面積は[１]なので、△アイウ→△ＰＧＦの面積は[２]ですね。

ここまでくれば、答えは目前です。

△ＰＢＣ：△ＰＣＤ＝ＢＰ：ＰＤ＝５：１です。
△ＤＰＣ＝△ＦＰＣの面積を[Ｘ]とおくと、△ＰＢＣ：△ＰＣＤ＝（[７]＋[Ｘ]）：[Ｘ]＝５：１となります。
すると、△ＰＢＣと△ＰＣＤの面積差５−１＝４が[７]にあたるので、[７]÷４＝[１.７５]がＸです。
ＢＧ：ＦＣ＝△ＰＢＧ：△ＰＦＣ＝[５]：[１.７５]＝２０：７です。

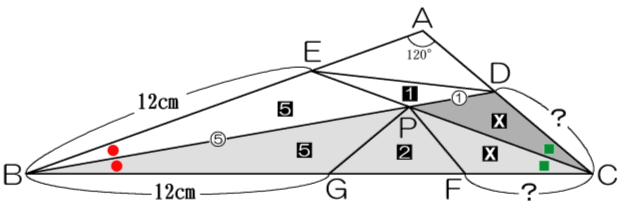
よって、ＦＣ＝ＣＤは１２×７÷２０＝４.２cmと求まります。

正解；２１／５[４.２]cm

問題に戻る