![]() 問72の解答
問72の解答
<解説>
一辺の長さがすべて整数で、縦の長さが3cmなので、一辺が1cm・2cm・3cmの正方形に切り分ける事になります。
少し考えると、切り分け方のパターンは次の4つしかないことはすぐにわかると思います。…★
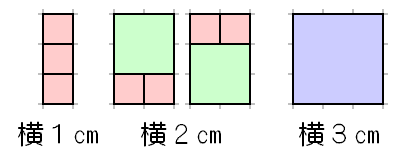
この4パターンの組み合わせを地道に調べていく方法もありますが、かなり面倒臭いです。
そこで、横の長さを段々長くして考えていくと、何かが分かるかもしれません。
長方形の横が1cm、2cm、3cmの場合は、次のようにそれぞれ1通り、3通り、6通りとなります。

では、横4cmの場合はどうでしょうか?
左の切り分け方が、★のどれになっているかに注目すると…
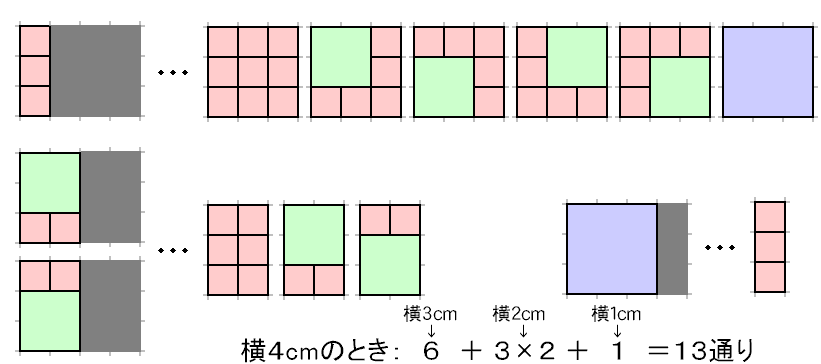
横4cmのときは、灰色部分の切り分け方のところが横1cm、2cm、3cmの場合を利用して、
(横4cmの切り方)=(横3cmの切り方)+(横2cmの切り方)×2+(横1cmの切り方)=6+3×2+1=13通り
となりますね。この考え方は横の長さがもっと長くなっても使えます。
そろそろ慣れましたか?
(横5cmの切り方)=(横4cmの切り方)+(横3cmの切り方)×2+(横2cmの切り方)=13+6×2+3=28通り

この要領で、次々に求めていくことができます。
(横6cmの切り方)=(横5cmの切り方)+(横4cmの切り方)×2+(横3cmの切り方)=28+13×2+6=60通り
(横7cmの切り方)=(横6cmの切り方)+(横5cmの切り方)×2+(横4cmの切り方)=60+28×2+13=129通り
(横8cmの切り方)=(横7cmの切り方)+(横6cmの切り方)×2+(横5cmの切り方)=129+60×2+28=277通り
(横9cmの切り方)=(横8cmの切り方)+(横7cmの切り方)×2+(横6cmの切り方)=277+129×2+60=595通り
(横10cmの切り方)=(横9cmの切り方)+(横8cmの切り方)×2+(横7cmの切り方)=595+277×2+129=1278通り
※中学生以上で学習する数列の表し方だと、以下のようになります。
縦3cm、横Ncmの切り分け方をA[N]と表すことにすると、N≧4のとき
A[N]=A[N-1]+2×A[N-2]+A[N-3]と表せます。
| N | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| A[N-1] | 6 | 13 | 28 | 60 | 129 | 277 | 595 |
| 2×A[N-2] | 6 | 12 | 26 | 56 | 120 | 258 | 554 |
| A[N-3] | 1 | 3 | 6 | 13 | 28 | 60 | 129 |
| A[N] | 13 | 28 | 60 | 129 | 277 | 595 | 1278 |
正解;1278通り |