算数限界編問79の解答

問題に戻る

＜解説＞

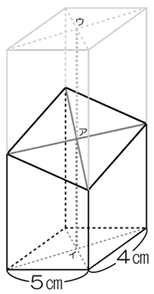立体の切断面を１つに定めるには、(同一直線上にない)３点が必要になります。
ところがこの問題には位置のわかる３点が直接与えられていません。そこで…

直方体を１回切断してできた立体α(切断面の形が平行四辺形,長方形,ひし形,正方形の場合)を考えます。

立体αを２つ(切断面がピッタリ重なるように)くっつけると、直方体βになります。
右図で、切断面の中心をア、直方体βの下面の中心をイ、直方体βの上面の中心をウとします。
すると、３点ウアイは一直線上にあり、しかもアは切断面の形によらず直線ウイの真ん中にあります。…★
例えば右図で、立体αの体積が２２０cm3であれば、イウは２２０×２÷(４×５)＝２２cm。
そしてアイの長さは、切断面の形によらず２２÷２＝１１cmです。

★をヒントにすると、立体Ｖの切断面が通る３点を見つけることができます。
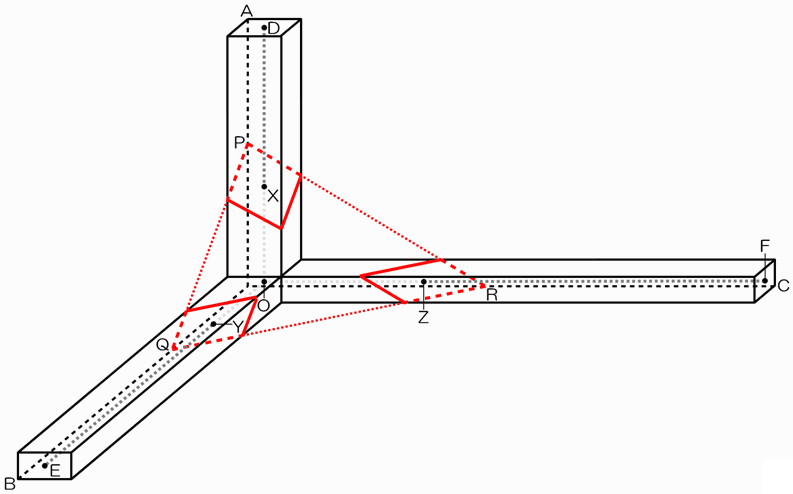
次の図は、立体Ｖの体積を４等分にしたときの様子です。
切断面が３か所ありますが、その形はすべて平行四辺形となります。

立体Ｖの体積は ４×５×５７＋６４×５×３＋４×９０×３＋４×５×３＝３２４０cm3。
４等分したときの１個ぶんは３２４０÷４＝８１０cm3です。
上の図のように、「立体Ｖの面の中心Ｄ・Ｅ・Ｆ」「切断面の中心Ｘ・Ｙ・Ｚ」を定めると、★より
┌
壱
└		 　８１０×２÷(４×５)÷２＝４０.５cm…ＤＸ
　８１０×２÷(３×５)÷２＝５４cm…ＥＹ
　８１０×２÷(３×４)÷２＝６７.５cm…ＦＺ
となり、切断面の通る３点Ｘ・Ｙ・Ｚの位置がわかりました！

さて、ＤＸ・ＥＹ・ＦＺの延長線は一点Ｏで交わりますが、その位置はＤやＥやＦの位置から考えて、
┌
弐
└		 　最左面(３点ＯＡＢを含む)の５÷２＝２.５cm右
　最奥面(３点ＯＡＣを含む)の４÷２＝２cm手前
　最下面(３点ＯＢＣを含む)の３÷２＝１.５cm上
にあります。また、△ＯＸＹや△ＯＸＺの辺の長さについては、壱と弐より
┌
参
└		 　５７＋３−(４０.５＋１.５)＝１８cm…ＯＸ
　６４＋４−(５４＋２)＝１２cm…ＯＹ
　９０＋５−(６７.５＋２.５)＝２５cm…ＯＺ
となっています。これはあとで相似な三角形として利用します。


さあ、いよいよ本格的に答えを求めにかかります。
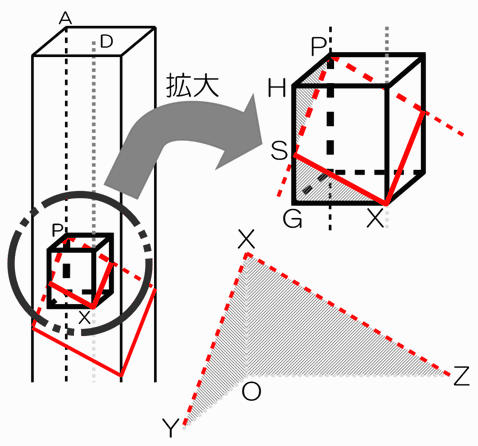
右図のように、ＰＸを対角線とする直方体Ｗを考えます。(もちろん、直方体Ｗも切断します)
直方体Ｗの頂点Ｇ・Ｈおよび切断面との交点Ｓを図のように定めます。
ＰＨ＝４÷２＝２cm、ＧＸ＝５÷２＝２.５cmですね。
目標は、ＸとＰの高さの差(つまりＨＧの長さ)を求めることです。

△ＨＳＰと△ＯＸＹは相似です。参より
　ＨＰ：ＨＳ＝ＯＹ：ＯＸ → ２：ＨＳ＝１２：１８ より、ＨＳ＝３cm。
△ＧＳＸと△ＯＸＺは相似です。参より
　ＧＳ：ＧＸ＝ＯＸ：ＯＺ → ＧＳ：２.５＝１８：２５ より、ＧＳ＝１.８cm。
よって、ＨＧ＝３＋１.８＝４.８cmとなります。


これでようやく、ＡＰの長さはＤＸより４.８cm短いとわかったので、ＡＰ＝４０.５−４.８＝３５.７cm！

なお、他の長さも調べると、ＢＱ＝５１.８cm、ＣＲ＝６１.２５cmなどとなり、立体Ｖは確かに４つに分かれることがわかります。

正解；３５.７[３５７／１０]cm

問題に戻る