問80の解答問80の解答
＜解説＞
「最短距離」の定石にどうやって持ちこむかがポイント。
草原と道路で速さが異なるため、このままでは単純に距離が最小のときというわけにはいきません。
どうにかして「草原だけ」を走ることに置き換えることができれば…
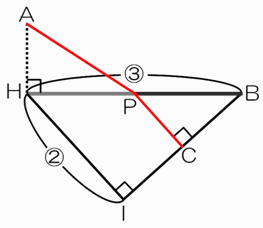秒速の比は草原：道路＝４ｍ：６ｍ＝２：３ですから、一定時間で走る距離の比は、草原：道路＝２：３ですね。→(α)
ここで、右図のように、ＨＩ：ＨＢ＝２：３となり、かつ角ＨＩＢ＝９０度となるような点Ｉを下側に取ります。
草原から道路に乗り換えるＨＢ上の地点をＰとして、ＰからＢＩに向けて垂線ＰＣを下ろします。
すると、ＰＢ(道路)を進むのにかかる時間は、ＰＣ(草原)を進むのにかかる時間と同じになります！
（理由）２角が等しいから△ＢＨＩと△ＢＰＣは相似で、ＰＣ：ＰＢ＝ＨＩ：ＨＢ＝２：３。そしてαより。
よって、草原ＡＰと道路ＰＢを走るのにかかる時間の和は、草原ＡＰ＋ＰＣを走るのにかかる時間と等しくなります。
では、草原ＡＰ＋ＰＣを走るのにかかる時間は、どういうときが最短になるのでしょう？
常に毎秒４ｍで進むので、ＡＰ＋ＰＣの長さを最短にすればいいわけですが。
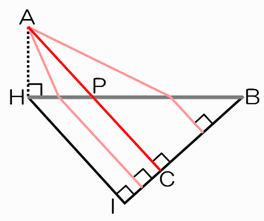右の図は、道路ＨＢ上のいろいろな場所に点Ｐを、ＩＢ上に点Ｃを取ったところを表します。
「最短距離」の定石より、線が折れ曲がったら最短距離にはなりません。
つまり、ＡＰ＋ＰＣの長さが最短になるのは、Ａ・Ｐ・Ｃが一直線に並び、かつＡＣがＩＢに対する垂線になるときです。(※)
ＡＨの長さが十分に短く、そしてＰやＣの取り方から、これは実現可能ですね。
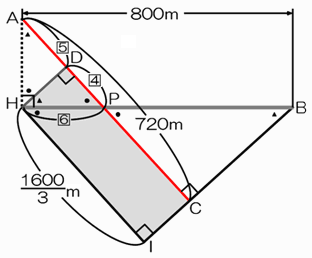ここからは普通の(？)平面図形の問題です。右図で同じ印の角度は同じ大きさです。
ＨからＡＰに向けて垂線ＨＤを下ろします。すると、△ＢＨＩ・△ＨＰＤ・△ＡＰＨはともに相似です。
ＨＩ：ＨＢ＝ＰＤ：ＰＨ＝ＰＨ：ＰＡ＝２：３です。(これより、ＨＩ＝１６００／３ｍがまずわかります)
ＰＤ＝[４]とすると、ＰＨ＝[６]、ＰＡ＝[９]となり、ＡＤ＝[９]−[４]＝[５]となることがわかります。→(β)
草原ＡＰと道路ＰＢを走るのにかかる時間の和が最短３分＝１８０秒になるのは、草原ＡＰ＋ＰＣを走って最短３分かかるときです。
草原での秒速は４ｍなので、直線ＡＣの長さは４×１８０＝７２０ｍです。
また、四角形ＤＨＩＣは、内角がすべて９０度なので長方形であり、ＤＣ＝ＨＩ＝１６００／３ｍです。→(γ)
βとγより、７２０−１６００／３＝５６０／３ｍが[５]にあたるので、[１]＝１１２／３ｍ。
実際に走った草原は１１２／３×[９]＝３３６ｍ。
また、[６]＝２２４ｍなので、実際に走った道路は８００−２２４＝５７６ｍです。
図形的に解かないのであれば、ＰＨ＝[２]、ＰＣ＝{２}とおくと、ＡＰ＝[３]、ＰＢ＝{３}となり、
[３]＋{２}＝７２０ｍ、[２]＋{３}＝８００ｍ、の消去算を解くのが一番楽だと思います。
もし、(※)が実現できなかったときを、念のため考えておきましょう。
ＡＨがとても長いとき(ＡからＢＩに向けて垂線を下ろすと、ＣがＢＩの延長線上にくるとき)は、道路を通らずに草原ＡＢを直線で進むときが最短になります。
このとき、ＡＢはＨＢ＝８００ｍより明らかに長く、かかる時間は８００÷４＝２００秒より長くなる(→３分より長い)ことから不適です。
正解；草原＝３３６ｍ，道路＝５７６ｍ |