![]() 問10の解答
問10の解答
<解説>
実際に図を書いてみるとかなり難しそうに見えますが、補助線をうまく引くと意外にあっさりと解けます。
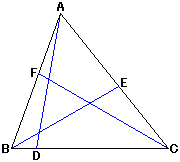
角ADB=99度より角ADC=180−99=81度、角BEC=99度より角BEA=81度、角CFA=99度より角CFB=81度です。
下図のように補助線を引いてみます(各頂点から向かいあう辺へ垂線を下ろします。補助線は赤い線です)。
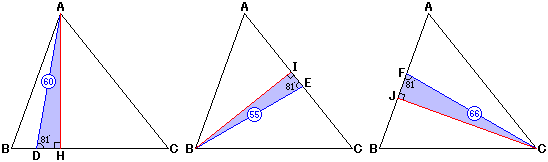
3つの直角三角形ADH・BEI・CFJは、2つの角度がそれぞれ等しいので相似です。
相似比は、問題文からAD:BE:CF=60:55:66です。
よって、AH:BI:CJ=60:55:66です。 …(※)
次に三角形ABCの面積を考えます。 三角形の面積の求め方は、当然「底辺×高さ÷2」ですね。
(三角形ABCの面積=)AB×CJ÷2=BC×AH÷2=AC×BI÷2
よってAB×CJ=BC×AH=AC×BIとなります。
さらに(※)からAB×66=BC×60=AC×55です。
したがって、AB:BC:AC=1/66:1/60:1/55 (AB,BC,ACにかけた数の逆数比)
これに60×55×66をかけると、
AB:BC:AC=60×55:55×66:60×66
これを簡単にすると、AB:BC:AC=10:11:12と出てきます。
なお、直角三角形ABHと直角三角形CBJが相似で、直角三角形ABIと直角三角形CAJが相似であることを利用してもいいでしょう。
正解;AB:BC:AC=10:11:12 |