![]() 問14の解答
問14の解答
<解説>
この問題のテーマは『展開図が正方形になる特殊な三角すい』です。
まずは切断面を考えます。
2つの平行な平面と、ある一つの平面とが交わってできる直線は平行になることに注意すると、切断面は下図のような台形PFHQ(詳しく言うと、“等脚台形”)になります。
直角二等辺三角形FGHと三角形PCQは相似ですから、三角形FGHは直角二等辺三角形なので、三角形PCQも直角二等辺三角形でCP=CQ。
CP=3cmなので、CQ=3cm。つまり、Qは辺CDの真ん中の点です。
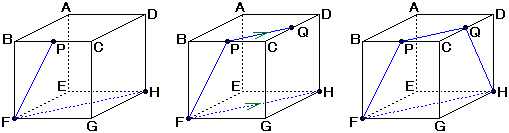
次に、FPとHQとGCをそれぞれ延長した線を考えてみます。
すると、これらの線は下図のように点Rで交わります。
2つの直角三角形・三角形RCQと三角形HDQは合同です(CQ=QD、角RCQと角HDQは直角、角RQC=角HQD)。 …(◆)
よって、RC=HD=6cmです。
切断面から点Gまでの高さを求めるのですから、答えを導く方針は‘三角すいR−FGHの体積を求め、面RFHを底面とした時の高さを求める’です。
まず三角すいR−FGHの体積は、 6×6÷2×12÷3=72cm3です。
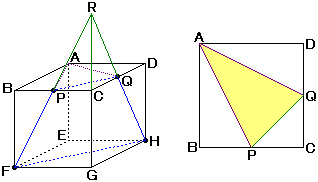
ここで三角すいR−PCQに注目してください。
AとP、AとQを結ぶと、三角形RPQと三角形APQは合同です(PQは共通、RP=AP、RQ=AQ ※RP、RQ、AP、AQはすべて「直角をはさむ2辺の長さが3cmと6cmの直角三角形の残りの一辺」)。
三角形APQの面積は、正方形ABCDから3つの直角三角形の面積を引き、 6×6−(3×6÷2×2+3×3÷2)=13.5cm2
よって、三角形RPQの面積も13.5cm2となります。
右上の正方形を、紫と緑の線を折り目として折ってみると、実は立体R−PCQと合同な立体ができます。 …(☆)
さらに、三角形RPQと三角形RFHは相似で、(◆)より相似比はRQ:RH=1:2です。
したがって、相似比は1×1:2×2=1:4ですから、三角形RFHの面積は13.5×4=54cm2です。
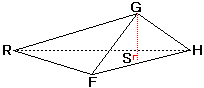
あとはもう簡単ですね。
54cm2×( ? )cm÷3=72cm3 を満たす( ? )を考えればよいのですから、
( ? )=4 と求まります。
(注)解説を見ると「算数限界編」でも使えそうなネタに見えますが、(☆)の立体は中学入試ではあまりに有名なため、こちらの方で出題しました。
正解;4cm |