問１７の解答

問題に戻る

＜解説＞

中学入試としては頻繁に出されるパターンですが、回転させる図形が変わった形なのでやや解きにくいでしょうか。

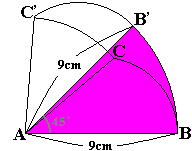
図形を回転させた図を書いてみると次のようになります。求める部分の面積は図の緑の部分です。

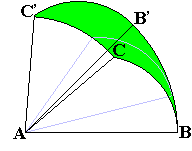
回転移動後のＢをＢ’、ＣをＣ’としています。
すると、角ＢＡＢ’＝４５度、角ＣＡＣ’＝４５度です。

これはどう見ても直接面積を求められそうにないので、「面積の足し引き」で考えてみましょう。
“全体から余分な部分を取り除く”ことを考えてみます。

すると、
=-
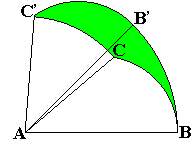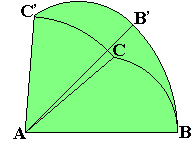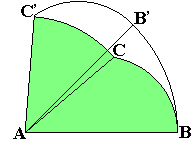
と表され、さらに
=+
=+
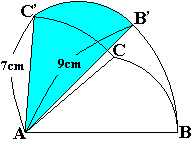
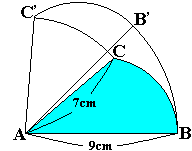ですから、
=
+- (+)
となります。

ここで、←この２つは同じものであることに注意すると、結局

=-
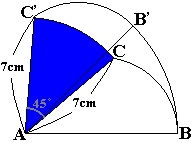
ということで、２つのおうぎ形の面積の差を求めればよいということがわかります。

よって、求める面積は、
９×９×３.１４×４５／３６０−７×７×３.１４×４５／３６０＝（９×９−７×７）×３.１４×１／８＝１２.５６cm²

問題に戻る