問１９の解答

問題に戻る

＜解説＞

今回は２通りの解法を紹介します。

[解法１]

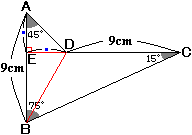
ＤとＢを結び、さらに、辺ＡＢ上に、角ＤＥＡ＝９０度となるような点Ｅを取ります（要するに、ＤからＡＢに垂線を下ろします）。
すると、三角形ＡＥＤは直角二等辺三角形であり、ＡＥ＝ＥＤです。　…（☆）

さて、四角形ＡＢＣＤの面積は、三角形ＡＢＤと三角形ＤＢＣの面積の和と考えることができ、その面積は、
９×ＥＤ÷２＋９×ＥＢ÷２＝９×（ＥＤ＋ＥＢ）÷２　となります。
ところが、（☆）より、ＥＤ＋ＥＢ＝ＡＥ＋ＥＢ＝９cmですから、求める面積は ９×９÷２＝４０.５cm² です。

[解法２]

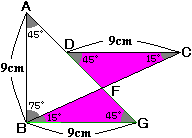
ＡＤの延長線とＢＣとの交点をＦとし、また、ＡＤの延長線上の点で角ＡＢＧ＝９０度となる点をＧとします。
すると、三角形ＡＢＧは直角二等辺三角形となり、ＢＧ＝ＡＢ＝９cmです。
また、角ＣＤＦ＝４５度、角ＦＢＧ＝１５度となります。
これらのことを考えると、三角形ＣＤＦと三角形ＢＧＦは合同になります（１辺とその両端の角がそれぞれ等しい）。　…（★）

さて、四角形ＡＢＣＤの面積は、三角形ＡＢＦと三角形ＤＦＣの面積の和ですが、（★）より、これは三角形ＡＢＦと三角形ＢＧＦの面積の和です。
つまり、直角二等辺三角形ＡＢＧの面積を求めればよく、 ９×９÷２＝４０.５cm² です。

問題に戻る