問２２の解答

問題に戻る

＜解説＞

この問題を解く前に、２つの準備が必要です。
とはいっても、どちらも中学入試では是非知っておきたい事柄なので、知っている方も多いでしょう。

----------

[有名な事実]〜接する２円の性質
２円が１点で外側で接している時、２円の中心を直線で結ぶと、その直線は２円の接点を通る。

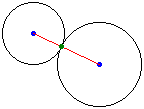
まあ当たり前といえることでしょう。
この事実は、図形のころがし移動でもおなじみですね。
無意識にこの事実を使って解いているはずです。

[有名な定理]〜線分比と面積比
下図の三角形ＤＢＥの面積と三角形ＡＢＣの面積の比は、ａ×ｃ：ｂ×ｄである。

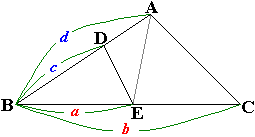
三角形ＡＢＥと三角形ＡＢＣは、底辺をそれぞれＢＥ、ＢＣと見ると、高さは等しいので、面積比は底辺比に等しくなるので、三角形ＡＢＥの面積と三角形ＡＢＣの面積の比はa：b。
また、三角形ＡＢＥと三角形ＤＢＥは、底辺をそれぞれＡＢ、ＤＢと見ると、高さは等しいので、面積比は底辺比に等しくなるので、三角形ＡＢＥの面積と三角形ＤＢＥの面積の比はc：d。
まとめると、三角形ＤＢＥの面積と三角形ＡＢＣの面積の比は、ａ×ｃ：ｂ×ｄ

----------

さて本題。
問題図の３円の中心（半径の大きい方から順にＰ、Ｑ、Ｒと名付けます）を結ぶと、[有名な事実]より、２円の接点を通ります。
また、２円の接点を、次の図のようにＸ、Ｙ、Ｚと名付けます。

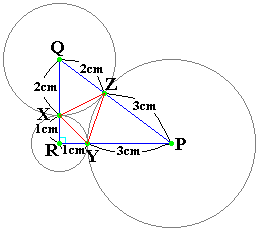
ＱＲ＝３cm、ＲＰ＝４cm、ＰＱ＝５cmとなることから、『辺の長さの比が３：４：５の三角形は直角三角形』なので、三角形ＰＱＲは、角ＰＲＱ＝９０度の直角三角形となり、面積は、４×３÷２＝６cm²です。

求めようとしている三角形ＸＹＺの面積は、三角形ＰＱＲから余分な三角形（三角形ＰＹＺ・ＱＸＺ・ＲＸＹ）を引きます。

[有名な定理]より、三角形の面積比を順次求めていきます。
　・三角形ＰＹＺ：三角形ＰＱＲ＝３×３：４×５＝９：２０
　・三角形ＱＸＺ：三角形ＰＱＲ＝２×２：３×５＝４：１５
　・三角形ＲＸＹ：三角形ＰＱＲ＝１×１：４×３＝１：１２

三角形ＰＱＲの面積を６０（２０と１５と１２の最小公倍数です）とすると、面積比
三角形ＰＱＲ：三角形ＸＹＺ＝６０：（６０−９×３−４×４−１×５）＝６０：１２＝５：１

ゆえに、三角形ＸＹＺの面積は、６×１／５＝６／５（＝１.２）cm²となります。

問題に戻る