問２４の解答

問題に戻る

＜解説＞

うまく補助線を引くとぐっと見通しが良くなる問題です。『ＡＢ＝ＣＤ』の条件を生かせるようにするには？

対角線ＢＤの真ん中の点をＱとし、ＱとＭ、ＱとＮを結びます。

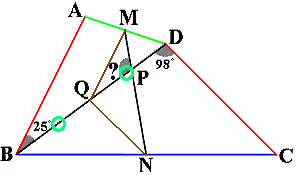
三角形ＡＢＤと三角形ＭＱＤは、ＡＤ：ＭＤ＝ＢＤ：ＱＤ＝２：１、角ＡＤＢ＝角ＭＤＱより、「２組の辺の比とその間の角が等しい」ので相似です。
同様に、三角形ＤＢＣと三角形ＱＢＮは、ＤＢ：ＱＢ＝ＣＢ：ＮＢ＝２：１、角ＤＢＣ＝角ＱＢＮより、「２組の辺の比とその間の角が等しい」ので相似です。
（注）これは要するに「中点連結定理」ですね。中学生以上はもちろん、上位校志望の小学生であれば知っているでしょう。

三角形ＡＢＤと三角形ＭＱＤは相似なので、ＡＢとＭＱは平行です。　…（ア）
また、三角形ＤＢＣと三角形ＱＢＮも相似なので、ＤＣとＱＮも平行です。　…（イ）

さて次の事柄が最大のポイント。「ＡＢ＝ＣＤ」という条件をうまく使います。
三角形ＡＢＤと三角形ＭＱＤの相似比は２：１ですから、ＭＱ＝１／２×ＡＢです。
また、三角形ＤＢＣと三角形ＱＢＮの相似比も２：１ですから、ＱＮ＝１／２×ＤＣです。
ところで、ＡＢ＝ＣＤですから、ＭＱ＝１／２×ＡＢ＝１／２×ＤＣ＝ＱＮです。
よって、三角形ＭＱＮは、ＱＭ＝ＱＮの二等辺三角形となります。　…（ウ）

ここまででわかったことを図にまとめてみましょう。

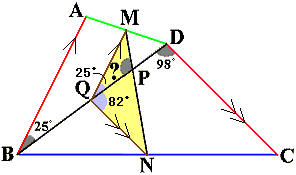
（ア）より角ＭＱＤ＝２５°、（イ）より角ＢＱＮ＝９８°なので角ＰＱＮ＝１８０−９８＝８２°です。
（ウ）より角ＱＭＮ＝角ＱＮＭであり角ＭＱＮ＝２５＋８２＝１０７°ですから角ＱＭＮ＝（１８０−１０７）÷２＝３６.５°とわかります。

よって、三角形ＭＱＰに注目すると、角ＭＰＱ＝１８０−（２５＋３６.５）＝１１８.５°（＝角ＭＰＢ）となります。

問題に戻る