問２７の解答

問題に戻る

＜解説＞

いろいろな解法が解法が考えられます。
今回は想定していた算数的解法の他に、送られてきた算数的解法もいくつか紹介します。

その前に、問題図についての条件をまとめておきましょう。

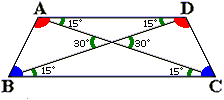
赤い色のつけた角（角Ａまたは角Ｄ）と青い色をつけた角（角Ｂまたは角Ｃ）の和は１８０度です。　…[☆]

[解法１]
台形ＡＢＣＤを三角形ＡＢＤと三角形ＤＢＣに分割し、次の図のようにくっつけ直してみます。

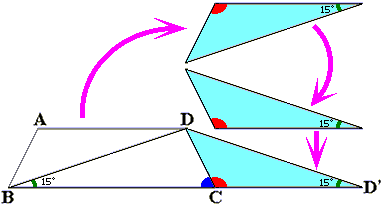
ＡＢ＝ＣＤと[☆]より、等しい２つの角が１５度、ＢＤ＝ＤＤ'＝１２cmの二等辺三角形ＤＢＤ'が完成します。

さて、この三角形の面積はどのように求めればいいかというと…有名な直角三角形が活躍します。

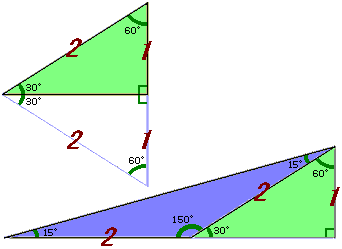
３つの角度がそれぞれ３０度、６０度、９０度の直角三角形は、図を見てもわかるように、正三角形を真っ二つにしたものです。
よって、この直角三角形の一番短い辺の長さは一番長い辺の長さの半分となります。　…[１]

これを利用すると、等しい２つの角が１５度の二等辺三角形の面積を求めることができます。
等しい２辺のうちの１辺を底辺と考えると、高さは底辺の長さの半分となることがわかります。　…[２]

というわけで、等しい２つの角が１５度、ＢＤ＝ＤＤ'＝１２cmの二等辺三角形ＤＢＤ'は、底辺を１２cmとすると[２]より高さは６cmとなり、
１２×６÷２＝３６cm²となります。

[解法２]

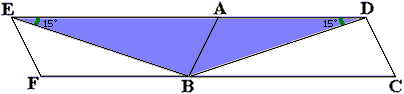
上の図は、台形ＡＢＣＤと合同な台形ＢＡＥＦを重ねた図です。
このときできた三角形ＢＤＥは、三角形ＤＢＣと三角形ＢＥＡは合同であることから、実は台形ＡＢＣＤの面積と等しいのです（三角形ＢＥＡを三角形ＤＢＣの部分に移動させてみましょう）。
しかも三角形ＢＤＥは解法１ででてきた二等辺三角形と合同です。
というわけで、面積は１２×６÷２＝３６cm²となります。

[解法３]

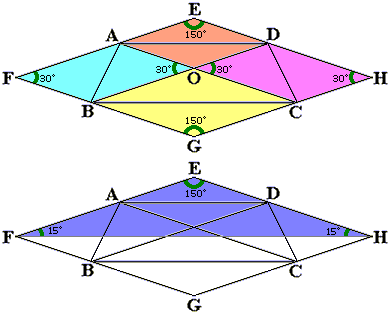
ＢＤに平行な直線のうち、頂点Ａと頂点Ｃを通るものをそれぞれ引き、ＡＣに平行な直線のうち、頂点Ｂと頂点Ｄを通るものをそれぞれ引いたものです。
すると、四角形ＥＦＧＨは１辺が１２cmのひし形であることがわかります。
ひし形ＥＦＧＨの面積は、台形ＡＢＣＤの面積の２倍です。（三角形ＥＡＤと三角形ＯＡＤ、三角形ＡＦＢと三角形ＢＯＡ、三角形ＢＧＣと三角形ＣＯＢ、三角形ＤＣＨと三角形ＣＯＤがそれぞれ合同であることから説明がつきます）
ここでＦとＨを結ぶと、ひし形ＥＦＧＨはちょうど２等分されます。　つまり、三角形ＥＦＨの面積がひし形ＥＦＧＨの面積の半分すなわち台形ＡＢＣＤの面積と等しいわけです。
というわけで、面積は１２×６÷２＝３６cm²となります。

[解法４]

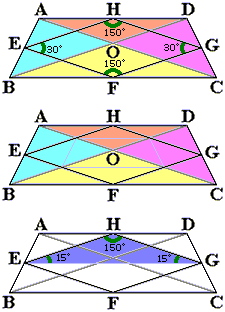
ＡＢの真ん中の点、ＢＣの真ん中の点、ＣＤの真ん中の点、ＤＡの真ん中の点をそれぞれＥ，Ｆ，Ｇ，Ｈとし、これら４点を結びます。
すると、中点連結定理から、ＥＦ，ＦＧ，ＧＨ，ＨＥの長さはともにＢＤあるいはＡＣの長さの半分で６cmです。
よって、四角形ＥＦＧＨはひし形です。
このひし形は、台形ＡＢＣＤの面積の半分です。これは解法４の真ん中の図のように図形を細切れにするとわかります。
ここで三角形ＨＥＧの面積を考えます。　三角形ＨＥＧの面積はひし形ＥＦＧＨの面積の半分ですから、三角形ＨＥＧの面積は台形ＡＢＣＤの面積の１／４倍です。
三角形ＨＥＧの面積は[２]より６×３÷２＝９cm²ですから、台形ＡＢＣＤの面積は９×４＝３６cm²です。

[解法５]

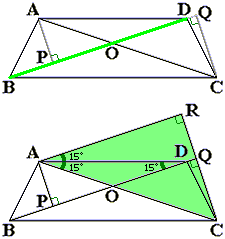
台形ＡＢＣＤの面積は、三角形ＡＢＤと三角形ＤＢＣの面積の和ですが、どちらも底辺をＢＤとみると、高さはそれぞれ図のＡＰとＣＱになります。
そこで、ＡＰとＣＱの長さの和を求めてみます。
Ａを通りＢＤの平行な直線を引き、ＣＱの延長線との交点をＲとします。
すると、ＡＲとＢＤは平行ですから、角ＡＲＣ＝９０度となりますから、四角形ＡＰＱＲは長方形です。
このことから、ＡＰ＝ＲＱとなるので、ＡＰとＣＱの長さの和は結局ＣＲの長さと等しくなります。
さて、角ＲＡＣ＝１５＋１５＝３０度ですから、三角形ＡＣＲは[１]で出てきた直角三角形ですから、ＣＲの長さはＡＣの長さの半分で６cmです。
したがって、台形ＡＢＣＤの面積は、１２×（ＡＰ＋ＣＱ）÷２＝１２×ＣＲ÷２＝１２×６÷２＝３６cm²です。

問題に戻る