問２９の解答

問題に戻る

＜解説＞

意外に手強く、思いこみにとらわれると痛い目にあってしまう問題かもしれません。

まずは、「輪郭が曲線の影」は、円柱のどの部分によってできた影なのかを考えます。

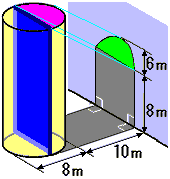
いきなり結論を書きますが、下図より、円柱の上底面の半分が、輪郭が曲線の影の正体であると分かります。（ただし、水色の直線は太陽光線を表しています。）
もし分かりにくければ、輪郭が直線部分の影が図の青い部分よりなることから納得してください。(^^;

ここからは横から見た図を利用します。

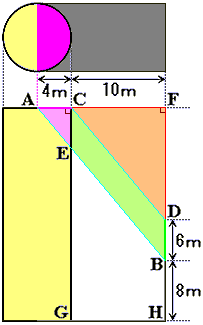
上図の２直線ＡＢとＣＤは太陽光線を表しています。ということは、ＡＢとＣＤは平行ですね。
従って、三角形ＡＢＦと三角形ＡＥＣは２角が等しいので相似です（角ＦＡＢ＝角ＡＣＥ＝９０度、平行線の同位角の性質より角ＦＡＢ＝角ＣＡＥ）
また、四角形ＣＥＢＤは、ＥＢとＣＤは平行、ＣＥとＤＢが平行なので平行四辺形ですから、ＣＥ＝ＤＢ＝６ｍです。

というわけで、三角形ＡＢＦと三角形ＡＥＣについて比例式を立てると、
ＡＣ：ＣＥ＝ＡＦ：ＦＢ　→　４：６＝１４：ＦＢ　より、ＦＢ＝６×１４÷４＝２１ｍ　です。

よって、ＦＨ＝２１＋８＝２９ｍ＝ＣＧ（つまり、建物の高さ！！）となります。

問題に戻る