問３２の解答

問題に戻る

＜解説＞

ちょっとしたことに気付けば、算数で解けますが、気付かなければとんでもない計算を強いられます。。

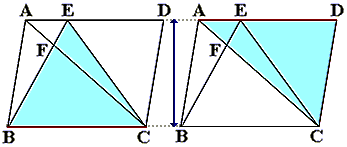
まず、三角形ＥＢＣと三角形ＡＣＤの面積は、底辺と高さはともに等しい長さなので、面積は同じですね。

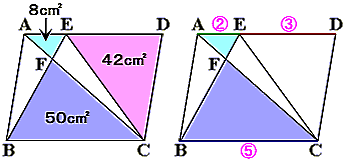
ここでちょっと三角形の面積を、
　三角形ＥＢＣ＝三角形ＥＦＣ＋三角形ＦＢＣ
　三角形ＡＣＤ＝三角形ＡＦＥ＋三角形ＥＦＣ＋三角形ＥＣＤ
と分けてみると、２つの三角形の面積は等しいのですから、

　三角形ＥＦＣ＋三角形ＦＢＣ＝三角形ＡＦＥ＋三角形ＥＦＣ＋三角形ＥＣＤ
となります。

　両辺から三角形ＥＦＣを引いて
三角形ＦＢＣ＝三角形ＡＦＥ＋三角形ＥＣＤ
となりますが、三角形ＦＢＣ＝５０cm²、三角形ＥＣＤ＝４２cm²だったので、
三角形ＡＦＥ＝８cm²となります。

ところで三角形ＡＦＥと三角形ＦＢＣは相似です（チョウチョ型相似）。
三角形ＡＦＥと三角形ＦＢＣの面積比は８：５０＝４：２５＝２×２：５×５なので、相似比は２：５とわかります。
（※相似比がａ：ｂの図形があったとき、面積比はａ×ａ：ｂ×ｂでしたね）

したがって、ＡＥ：ＢＣ＝２：５となり、ＡＥ：ＥＤ＝２：５−２＝２：３です。

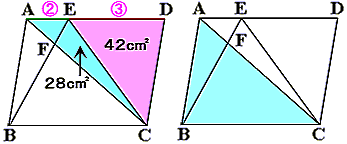
三角形ＡＣＥの面積は４２×２／３＝２８cm²です。（三角形ＡＣＥと三角形ＥＣＤの面積比はＡＥ：ＥＤ）
これにより、三角形ＡＣＤの面積は２８＋４２＝７０cm²と求まります。
三角形ＡＣＤの面積は平行四辺形の半分でしたから、答えはこの２倍で１４０cm²となります。

問題に戻る