問３４の解答問３４の解答
＜解説＞
中学入試としては標準的な問題です。
あまり新鮮な問題というわけでもないので、今回は解き方を３つほど紹介することにします。
（その１）
「サトシ＋タケシの速さ」で池を一周すると４０分かかり、「カスミ＋タケシの速さ」で池を一周すると４４分かかることになるので、速さの比はかかる時間の逆比になります。
「サトシ＋タケシの分速」：「カスミ＋タケシの分速」＝４４：４０＝１１：１０とわかります。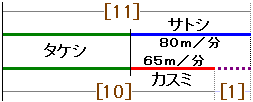
このことから、サトシの分速とカスミの分速の差…つまり８０−６５＝１５ｍが１１−１０＝[１]にあたります。
（これがわかりにくければ、右の線分図を参考にしてください。）
「サトシ＋タケシの分速」、つまり[１１]の速さでは４０分で池を一周するので、１５×１１×４０＝６６００ｍが答えです。
（その２）
池一周分を３人で走った道のりを個別に線分図で表すと次の図のようになります。
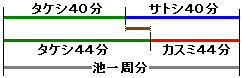図で茶色の部分に注目します。
茶色部分の長さは、サトシとカスミの進んだ道のりの差で表すと、８０×４０−６５×４４＝３４０ｍとなります。
一方、タケシだけを見てみると、茶色部分はタケシが４分で進んだ道のりであることがわかります。
つまり、タケシは３４０ｍを４分で進んだことになるので、タケシの分速は３４０÷４＝８５ｍとわかります。
あとは簡単。（８５＋８０）×４０＝６６００ｍ または（８５＋６５）×４４＝６６００ｍと求められます。
（その３）
サトシとカスミは、１分につき８０−６５＝１５ｍずつ離れていく（もちろんカスミが後ろになる）ので、サトシとタケシが出会ったとき、カスミは１５×４０＝６００ｍ後ろにいることになります。これは、このときのタケシとカスミは６００ｍ離れているということになります。
タケシとカスミは、この４分後に出会いました。つまり、２人は１分につき６００÷４＝１５０ｍずつ近づくということです。
タケシとカスミは同時に出発して４４分で出会っているので、１５０×４４＝６６００ｍ、とすれば池の一周が求まりますね。
正解；６６００ｍ |