![]() 問36の解答
問36の解答
<解説>
まず、合同な2つの三角形について整理しておきましょう。

合同な図形は、対応する頂点に注意しましょう。
「三角形ABCと三角形EADは合同な三角形」というと、三角形ABCの頂点Aに対応するのは三角形EADでは頂点E、…という風に決まっています。
三角形EADにおいて角ADEは、三角形ABCでは角BCAに対応しますから、角BCA=角ADE=40度。(同様に、角EAD=角ADE=40度)
つまり、三角形ABCと三角形EADは、AB=AC = EA=EDの二等辺三角形なんです。 …(☆)
では、本題に入ります。
CとEを結んだ図を考えます。。
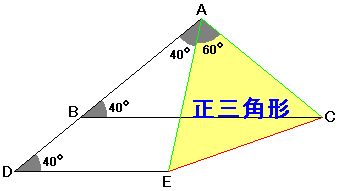
角EAD=40度、角BAC=180−40×2=100度なので、角EAC=60度です。
ところで(☆)より、AE=ACですね。
このことから、三角形AECは正三角形であることがわかりますね!
というわけで、角AEC=60度、EC=DEであることがいえます。 …(★)
あとは計算するだけです。
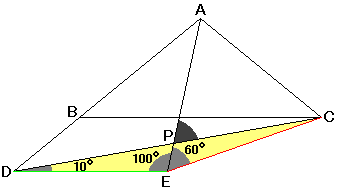
(★)より、三角形DECは二等辺三角形で、角DECは100+60=160度ですから、角CDE=(180−160)÷2=10度。
よって、角APC=角DPE(対頂角の性質ですね)
=180−(10+100)=70度、と求まります。
| 正解;70度 |