問40の解答

問題に戻る

＜解説＞

まず、角度を書き込んでいきましょう。
三角形ＥＣＤは、ＣＡ＝ＣＥの二等辺三角形より、
角ＣＡＥ＝角ＣＥＡ＝３９＋４３＝８２度。　角ＥＣＡ＝１８０−８２×２＝１６度。

…しかし、角度は普通に書き込めるのはここまでです。
そこで、ちょっと工夫してみます。
ＣＡ＝ＣＥであることに着目して…

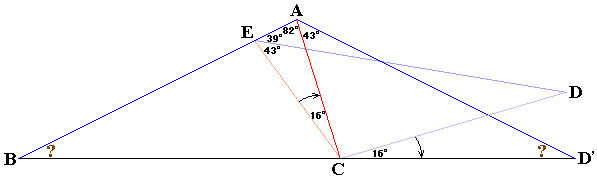
三角形ＡＣＤを、Ｃを中心に１６度回転させると上図のようになります。

ＣＡ＝ＣＥ、角ＥＣＡ＝１６度より、移動後のＥはＡと重なります（というか、そうなるように回転移動した）。

そしてＣＤも、Ｃを中心に１６度回転することになりますから、移動後の点ＤをＤ'とすると、
角ＢＣＤ'＝１６４＋１６＝１８０度。
というわけで、実は３点Ｂ・Ｃ・Ｄ'は一直線上に並ぶのです。

つまり、「回転移動」することによって、三角形ＡＢＤ'ができたことになります。
さらに都合のいいことに、ＡＢ＝ＡＤ'ですから、三角形ＡＢＤ'は二等辺三角形です（角ＡＢＤ'＝角ＡＤ'Ｂ）

二等辺三角形ＡＢＤ'において、角ＢＡＤ'＝８２＋４３＝１２５度。
したがって角ＡＢＤ'は　（１８０−１２５）÷２＝２７.５度　です。

問題に戻る