![]() 問44の解答
問44の解答
<解説>
BPの延長線とADの延長線の交点をQとします。相似や特殊図形の発見ができるかどうか…
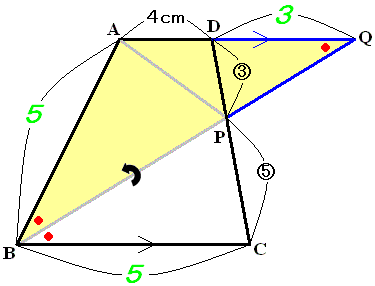
BPを折り目として三角形BCPを折り返すと、移動後のCは頂点Aにピッタリ重なったので、BC=BAです。
また、角PBC=角PBAですね。
次に、ADとBCが平行なので、“平行線の錯角”より、角QBC=角BQA。
よって角ABQ=角AQBとなり、三角形ABQはAB=AQの二等辺三角形です。
また、ADとBCが平行なので、三角形PBCと三角形PQDは(いわゆるチョウチョ型)相似です。
相似比は、PC:PD=5:3。 したがってBC:QDも5:3となります。
このことからBC=5、QD=3とおくと、
AB=BC=5、AQ=4+3です。
三角形ABQはAB=AQの二等辺三角形でしたから、結局 5=4+3 です。
よって、2=4cmですから、1=2cm。
求めたいのはBCですから、2×5=10cmとわかります。
正解;10cm |