問47の解答

問題に戻る

＜解説＞
最大のポイントはやはり「三角形ＡＢＥの面積と四角形ＤＢＥＦの面積が等しい」をどう生かすか、です。

下図のように、ＤとＥを結んで考えます。

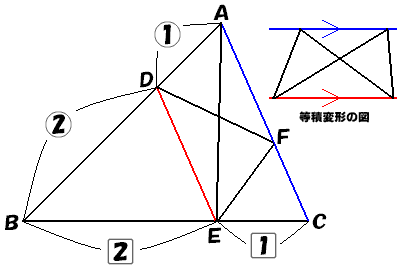
面積の等しい２つの図形…三角形ＡＢＥと四角形ＤＢＥＦ…は、
　三角形ＡＢＥ＝三角形ＤＢＥ＋三角形ＡＤＥ
四角形ＤＢＥＦ＝三角形ＤＢＥ＋三角形ＦＤＥ
と表すことができます。両方とも三角形ＤＢＥを含んでいるので、
三角形ＡＤＥと三角形ＦＤＥの面積が等しいことがいえます。

ところで三角形ＡＤＥと三角形ＦＤＥは、底辺がＤＥで共通です。
それで面積が等しいということは…何かを連想しませんか？
そう、これって「底辺と高さが等しい三角形の等積変形」そのものなんですね。
すなわち、ＤＥとＡＣが平行であることを意味します。

さきほどわかったことから、三角形ＢＥＤと三角形ＢＣＡは相似です。
そのことから、ＢＥ：ＥＣ＝ＢＤ：ＤＡ＝２：１です。
よって、三角形ＡＢＥの面積は、底辺比と面積比の関係により６０×２／３＝４０cm²。
つまり、四角形ＤＢＥＦの面積も４０cm²です。

三角形ＡＢＣ＝四角形ＤＢＥＦ＋三角形ＦＥＣ＋三角形ＡＤＦと分割できますから、
６０＝４０＋７＋三角形ＡＤＦ　より、三角形ＡＤＦは１３cm²とわかりますね。

問題に戻る