![]() 問55の解答
問55の解答
<解説>
 まずは超有名定理の確認。
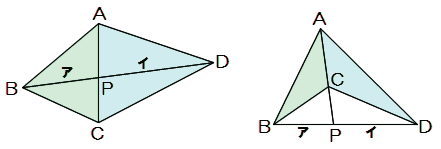
まずは超有名定理の確認。
次の図において、BP:PD=ア:イのとき、面積比△ABC:△ACDはア:イになります。(★)
これは、△ABP:△APDも△BCP:△PCDもア:イであることから容易に導けます。
 今回の問題に、さっそくさきほどの★を使いましょう。
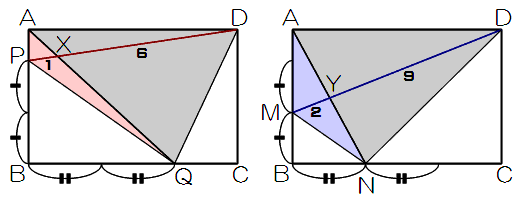
今回の問題に、さっそくさきほどの★を使いましょう。
PX:XD=1:6より、△APQ:△AQD=1:6 …(甲)
MY:YD=2:9より、△AMN:△AND=2:9 …(乙)
ところで、(甲)(乙)の△AQDと△ANDはともに長方形ABCDの半分なので、面積は等しいですね!
そこで、△AQD=△AND=[18](6と9の最小公倍数)と置き直してみます。
すると、△APQ=[3]、△AMN=[4]ですね。
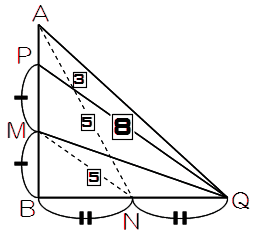 △AMQの面積は、△AMNと比べて、底辺AMは共通・高さBQはBNの2倍なので、[4]×2=[8]。
△AMQの面積は、△AMNと比べて、底辺AMは共通・高さBQはBNの2倍なので、[4]×2=[8]。
△APQ=[3]、△PMQ=[8]−[3]=[5]なので、AP:PM=3:5。
PM=MBですから、AP:PB=3:5×2=3:10です。
正解;3:10 |