問57の解答問57の解答
＜解説＞
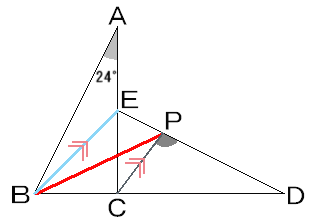ＢとＥを結んで考えます。
四角形ＡＢＣＤの面積は、三角形ＡＢＣの面積２つぶんなので、半分ずつに分けた図形の面積は、どちらも三角形ＡＢＣの面積と等しくなります。
つまり、２等分してできた凹四角形ＡＢＰＥは、三角形ＡＢＣの面積と等しいわけです。
さて、三角形ＡＢＣを凹四角形ＡＢＰＥに等積変形するには、三角形ＡＢＥは共通ですからそれ以外の部分を等しくする、すなわち三角形ＥＢＣを三角形ＥＢＰに変えればよいことが図よりわかります。
三角形ＥＢＣと三角形ＥＢＰは面積が等しく、しかも底辺ＢＥは共通ですので、ＢＥとＣＰは平行であることが分かります。
（そうでないと、高さは等しくなりませんよね！）
というわけで、三角形ＥＢＣが直角二等辺であることと平行線の錯角（通称：Ｚ法則）より、角ＥＣＰ＝角ＢＥＣ＝４５度。
ゆえに角ＣＰＤは三角形ＥＣＰの角Ｐの外角より、角ＣＥＰ＋角ＥＣＰ。
角ＣＥＰ＝１８０−（９０＋２４）＝６６度だから、答えは６６＋４５＝１１１度、となります。
正解；１１１度 |