算数実戦編問59の解答

問題に戻る

＜解説＞

正三角形のワクをクギに引っかけていろいろ動かしてみると、ワクの通過する部分は、図１の右下のようになります。

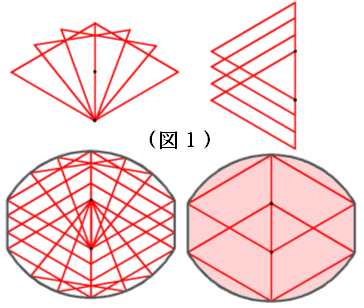
なんだかラグビーボールが肥満化したようなびみょーな形ですので、ここは図形を分割して考えてみましょう。

分割する前に、図２左側の灰色の三角形に注目してください。
４つとも正三角形であることはすぐに分かると思います。
また、クギの間隔が７.５cmであることから、中心部の２つの正三角形の一辺は７.５cmです。
ということは、両サイドの２つの正三角形の一辺も１５−７.５＝７.５cmです。
これら４つの合同な正三角形をうまく利用する為に、図２右側のように図形を分割します。

右上にあるのは、もちろん半径１５cm、中心角６０×２＝１２０度の扇形です。
右下の図形は、両サイドの正三角形を中心部に寄せ集めれば、右上の扇形と同じものが出来上がります。
結局求める面積は、半径１５cm、中心角１２０度の扇形２つ分です。

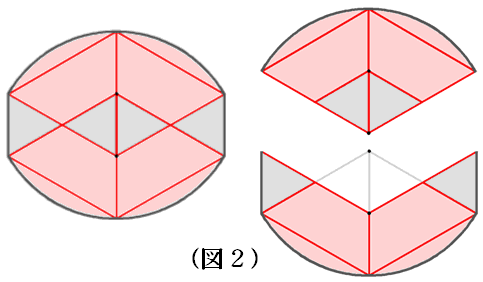
中心角１２０度の扇形は、３つくっつければ円になりますから、
１５×１５×３.１４÷３×２＝１５０×３.１４＝４７１cm2となります。

正解；４７１cm2

問題に戻る