問62こたえ

戻る

まずは、例にある８枚のカードを切ったときのカードの推移を観察しましょう。

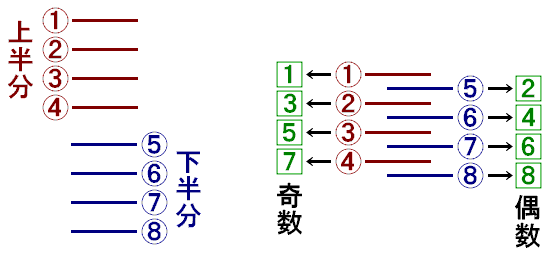
さて本題。まず「はじめは５５番目のカード（カードＰと名付ける）」が上半分にいるのか下半分にいるのか検証しましょう。
２回目の操作後のＰの位置は５５番目＝奇数番目なので、★より２回目の作業前には上半分にあったことがわかります。
そしてＰははじめと２回目の作業後は同じ位置にあるのですが、このときＰは下半分にあります。
はじめ上半分にあるとすれば、操作１回後も上半分にあるので、☆よりカードはどんどん下に移り元に戻らないからです。
以上より、（はじめ）-（操作１回後）-（操作２回後）のＰの位置は（下半分）-（上半分）-（下半分）であることがわかります。

以上のことを踏まえ、操作を逆から考えて解いてみます。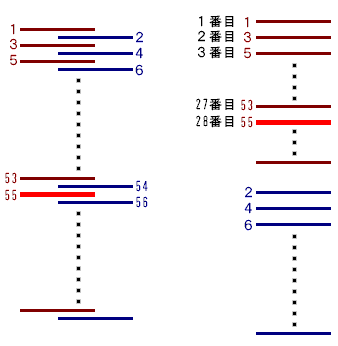

２回目の操作前には上半分のどこかにあったカードＰは、操作後には上から５５番目に移りました。
上半分のカードの上から１番目、２番目、３番目、…のカードはそれぞれ１番目、３番目、５番目、…と奇数番目に移ります。
５５は （５５＋１）÷２＝２８ より２８番目の奇数ですから、２回目の操作前には上から２８番目にありました。

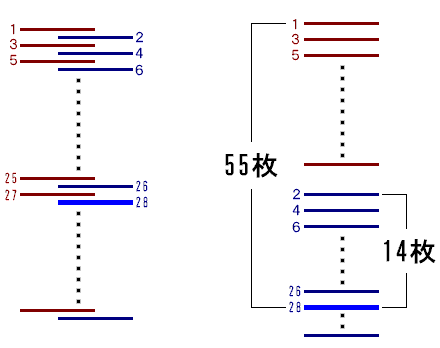では、同様にして１回目の操作前を考えてみましょう。 １回目の操作前には上から５５番目にあったカードＰは、操作後には上から２８番目に移りました。
下半分のカードの上から１番目、２番目、３番目、…のカードはそれぞれ２番目、４番目、６番目、…に移ります。
２８は１４番目の偶数ですから、下半分の上から１４番目にあるカードだとわかります。
ところで、このことから上半分にあるカードが５５−１４＝４１枚であることがわかります。
よって、カードの枚数は４１×２＝８２枚ですね。

方程式が扱えるなら、次の性質を利用してもいいでしょう。
Ｎ枚のカードを１回「切る」と、上からｐ番目のカードは
はじめ上半分にあったら（２×ｐ−１）番目、下半分にあったら（２×ｐ−Ｎ）番目に移る

一番下のカードは常に同じ位置にいますが、５５は奇数なので明らかに一番下ではないですね。

戻る