問72の解答

問題に戻る

＜解説＞

正方形の面積を、うまく相似にからめられるかどうかがカギ。

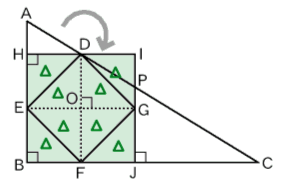点Ｄから辺ＡＢに向けて垂線ＤＨを下ろします。
このときできた△ＡＨＤを、点Ｄを中心に１８０度回転させてできた三角形をＰＩＤとします。…◆
明らかに３点ＨＤＩは一直線上に並び、点Ｐは辺ＡＣ上にきます。

さらに、点Ｉから辺ＢＣに向けて垂線ＩＪを下ろします。

すると、四角形ＨＢＪＩは、正方形ＤＥＦＧの面積の２倍の正方形です。…★
条件より、角ＥＦＢ＝角ＧＦＪ＝(１８０−９０)÷２＝４５度。
これと角ＦＥＯ＝４５度などから、ＨＩとＥＧとＢＪは平行。
これらのことから、△の印のついた三角形は全て合同な直角二等辺三角形です。
以上のことから★が言えます(細かい証明は省略^^;)。

ところで、ＰＪとＡＢは平行ですから、△ＣＡＢと△ＣＰＪは相似です。
◆より、台形ＡＢＪＰは正方形ＨＢＪＩに変形でき、その面積は★より８４×２＝１６８cm²。
△ＣＰＪの面積は２００−１６８＝３２cm²です。

△ＣＡＢと△ＣＰＪの面積比は２００：３２＝２５：４＝５×５：２×２です。
相似な図形の面積比は「(相似比)×(相似比)」に等しいので、△ＣＡＢと△ＣＰＪの相似比は５：２ですね！

ＢＣの長さを[５]とすると、ＢＦ＝([５]−[２])÷２＝[１.５]、ＦＣ＝[５]−[１.５]＝[３.５]ですね。
というわけで、ＢＦ：ＦＣ＝３：７です。

問題に戻る