![]() 問2解答
問2解答
<解説>
まず「信号で2回だけ止まる」にはどこで止まればよいかを考えてみましょう。
自動車(以下”車”)がAを出発してはじめてある地点(B,C,D,E,Fのどれか)の信号で止まったとします。
車は信号が青になるまでは止まったままです。そして信号が青になって再出発してからも最初と同じ時速で走ります。
しかも信号はすべて等間隔で並んでいますから、信号が青になって再出発するという状況はAを出発したときと同じ状況です。
つまり、1度信号で止まってからは「Aを出発してはじめて信号で止まって再出発する」までと同じことを繰り返すということがわかります!
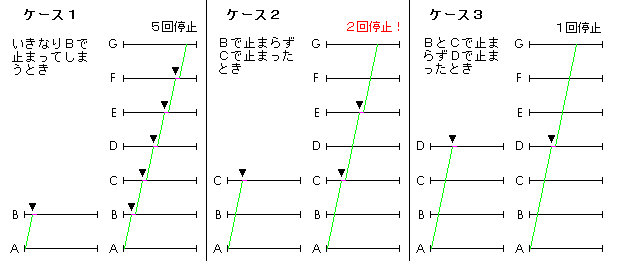
下の(図1)から、Bで止まらずCで止まれば必ず信号で2回だけ止まってGに着くことがわかります。
(下図にはB,C,Dで止まらずEで止まったときなどのケースが書いてありませんが、ケース3を見れば1回しか停止しないことは明らかでしょう)
(図1)
それでは条件にあう車の時速を求めてみましょう。(図2)を見てください。
が青信号&黄信号、つまり止まらずに通過できる範囲、
が赤信号、つまり止まらなければならない範囲を表しています。
(図2)
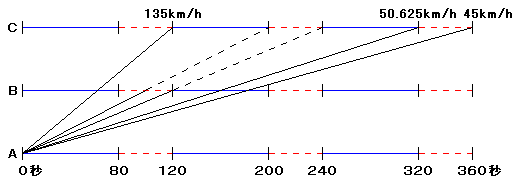
AC間の距離は 2250×2÷1000=4.5km です。
信号は 75秒間は青→5秒間は黄→40秒間は赤 と120秒の周期でいっせいに切り替わります。
C地点に着いたとき、信号が赤になるようにするには、Aを出発してから
80秒〜120秒、200秒〜240秒、320秒〜360秒、…
でC地点に着けばいいことが(図2)からもわかります。
1) Aを出発してから80秒〜120秒かかってCに着いたとき
この場合、B地点の信号は必ず青で通過することは明らかですが、120秒かかってCに着いたとしても、
時速は 4.5÷120×60×60=135km で、時速100kmを越えてしまいますから、不適です。
2) Aを出発してから200〜240秒かかってCに着いたとき
この範囲で止まることはできません。なぜなら、この範囲で止まろうとすると、B地点に着くまでにかかる時間の範囲はC地点に着くまでの半分の100〜120秒であり、このときはB地点の信号が赤ですから(Aを出発してから80秒〜120秒は全地点の信号が赤)、200〜240秒かかってCに着くには、Bの赤信号を強行突破しなければならないからです。(注:240秒かかってCに着いたときは信号に1度もかかりません)
3) Aを出発してから320秒〜360秒かかってCに着いたとき
B地点に着くまでにかかる時間の範囲は、2)
から160秒〜180秒です。このときはBの信号は青です。
320秒かかってCに着いたとすると、時速は 4.5÷320×60×60=50.625
50.625を越えない整数のうち最大のものは50ですから、時速50kmが有力な候補となります。
しかしもしかすると360秒かかってCに着いたときの時速が50kmより多いかもしれないので、このときの時速を求めると
4.5÷360×60×60=45
時速50kmは45km〜50.625kmの間に入っています!
あとはAを出発してからGに着くまでの時間を求めるだけです。
Aを出発してからCの信号で止まって再出発するまで、Cを出発してからEに止まって再出発するまでにかかる時間は(図2)から各360秒。
Eを出発してGに着くまでにかかる時間は、EG間の距離は2250×2÷1000=4.5kmなので、
4.5÷50×60×60=324秒。
よって360×2+324=1044秒=17分24秒
正解;17分24秒 |