![]() 問6解答
問6解答
<解説>
条件が非常に複雑です。ダイヤグラムを書いてみましょう。
キョウコさんが上りの途中で川を下ってくるトモノリさんに出会う地点をDとします。
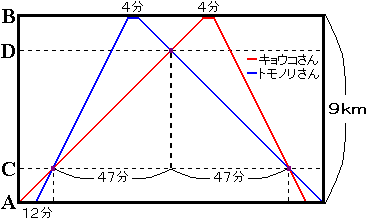
キョウコさんはCからBへ上り、4分休んでからBからCへ下るのに47+47=94分かかっていますから、キョウコさんがBからCへ下るのにかかった時間は、94−4−(CからBへ上るのにかかった時間)=90−(CからBへ上るのにかかった時間)です。
一方、トモノリさんもCからBへ上り、4分休んでからBからCへ下るのに47+47=94分かかっていますから、トモノリさんがCからBへ上るのにかかった時間は、94−4−(BからCへ下るのにかかった時間)=90−(BからCへ下るのにかかった時間)です。
次に、CD間の場合を考えます。
キョウコさんはCからDへ上るのに47分、トモノリさんはDからCへ下るのに47分かかっています。
このとき2人は同じ距離を同じだけ時間をかけて進んでいますから、キョウコさんがCからBへ上る時間と、トモノリさんがBからCへ下る時間も同じです…(A)
このことから、キョウコさんがBからCへ下る時間とトモノリさんがCからBへ上るのにかかる時間は等しいことがわかります…(B)
さて、(A)では2人は同じ距離を進むのに同じだけ時間がかかっていますから、キョウコさんの上る速さ=トモノリさんの下りの速さ、つまり(キョウコさんのボートの静水時の速さ)−(川の流れの速さ)=(川の流れの速さ)です…(C)
また、(B)でも2人は同じ距離を進むのに同じだけ時間がかかっていますから、キョウコさんの下る速さ=トモノリさんの上る速さ、つまり(キョウコさんのボートの静水時の速さの半分)+(川の流れの速さ)=(トモノリさんのボートの静水時の速さ)−(川の流れの速さ)です…(D)
ここで川の流れの速さを[1]とします。
(C)は(キョウコさんのボートの静水時の速さ)−[1]=[1]となり、キョウコさんのボートの静水時の速さ=[2]となります。
(D)は[2]÷2+[1]=(トモノリさんの静水時の速さ)−[1]となり、トモノリさんの静水時の速さ=[3]となります。
また、キョウコさんの上りの速さとトモノリさんの下りの速さはともに[1]、キョウコさんの下りの速さとトモノリさんの上りの速さはともに[2]です。
キョウコさんが上る速さは[1]、キョウコさんの下る速さは[2]なので、キョウコさんがCからBへ上るのにかかる時間とキョウコさんがBからCへ下るのにかかる時間の比は速さの比とは逆比になって2:1となります。
キョウコさんはCからBへ上り、BからCへ下るのに90分かかっていますから、キョウコさんがCからBへ上るのにかかる時間は90×2/(2+1)=60分です。
では、トモノリさんのボートの静水時の速さを求めましょう。
キョウコさんはAからBの距離9kmを上るのに12+60=72分かかっていることになるので、キョウコさんの上りの時速は9÷72×60=7.5km/h。これが[1]にあたります。
トモノリさんのボートの静水時の速さは[3]ですから、7.5×3=22.5km/hがトモノリさんのボートの静水時での速さですね。
次にキョウコさんがAを出発してからAに帰りつくまでにかかった時間を求めます。
まずキョウコさんがAからBへ上るのにかかる時間は前に求めたように72分。
また、キョウコさんが上る速さは[1]、キョウコさんの下る速さは[2]なので、キョウコさんがAからBへ上るのにかかる時間とキョウコさんがBからAへ下るのにかかる時間の比は速さの比とは逆比になって2:1となります。
よって、キョウコさんがBからAへ下るのにかかる時間は72×1/2=36分。
したがって、キョウコさんがAを出発してからAに帰りつくまでにかかった時間は、72+4+36=112分。
正解;(1)22.5km/h (2)112分 |