![]() 問18の解答
問18の解答
<解説>
3台の列車の様子をダイヤグラムに書いた後は、普通の旅人算として解こうとするとわけがわからなくなります。他の方法を考えましょう。
まずは3台の列車がA駅からB駅まで行く様子をダイヤグラムに表してみましょう。
なお、−は普通列車、 −は急行列車、 −は特急列車を表します。
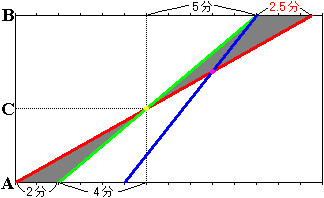
急行列車が普通列車に追いつく地点をCとします。
急行列車が出発してからCに来るまでに4分、CからB駅に着くまでに5分かかっています。
列車は一定の速さで進むので、AC間とCB間の距離の比は4:5になります。
そして、図で灰色の2つの三角形は相似で、相似比は4:5となります。
したがって、普通列車がB駅に着くのは、急行列車と特急列車がB駅に着いてから
2×5/4=2.5分後であるとわかります。
…ここまでが準備。
これより、本題である「1台目の列車が通ってから2台目の列車が通るまでの時間と、2台目の列車が通ってから3台目の列車が通るまでの時間が等しくなる2地点を見つけ出す」作業に入りますが、このままの図では、その地点を探すのは容易ではありません。
そこで、ダイヤグラムに架空の列車を上手く走らせてみると、その2地点が明快に得られます。
以後、−は架空の列車を表すものとします。
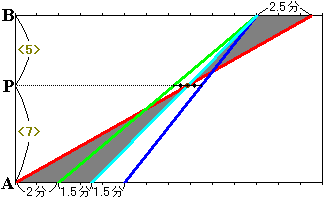
この図は、最初のダイヤグラムに、常に急行列車と特急列車の中間地点を通る“幽霊列車1号”を走らせたものです。
すると、幽霊列車1号が普通列車に追いつく地点Pが、「急行列車が通ってから普通列車が通るまでの時間と、普通列車が通ってから特急列車が通るまでの時間が等しくなる地点」であることがわかりますね。
この図で灰色の2つの三角形は相似で、相似比は(2+1.5):2.5=7:5です。
よって、AP間とPB間の距離の比は7:5です。
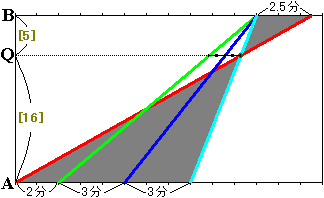
次に、最初のダイヤグラムに“幽霊列車2号”を走らせてみます。これは、特急列車より後に出発し、急行列車が通ってから特急列車が通るまでの時間と、特急列車が通ってから幽霊列車2号が通るまでの時間が常に等しくなるようにします。
すると、幽霊列車2号が普通列車に追いつく地点Qが、「急行列車が通ってから特急列車が通るまでの時間と、特急列車が通ってから普通列車が通るまでの時間が等しくなる地点」であることがわかります。
図で灰色の2つの三角形は相似で、相似比は(2+3+3):2.5=16:5です。
よって、AQ間とQB間の距離の比は16:5です。
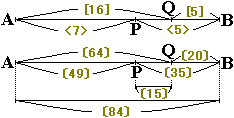
さて、ここでAB間の距離を、7+5=12と16+5=21の最小公倍数の〔84〕としてみます。
すると、AP=〔49〕、PB=〔35〕、AQ=〔64〕、QB=〔20〕となります。
従って、PQ間の距離は〔64〕−〔49〕=〔15〕と表されるので、AB間の距離とPQ間の距離の比は84:15=28:5となります。
よって、AB間の距離は、 1800×28/5=10080mと求まります。
正解;10080 |