問２１の解答問２１の解答
＜解説＞
無計画にボタンを押すのでは、ライトを全部点灯させられるかどうかも怪しいですね。
『なるべく多くのボタンを押す＝押さないボタンはなるべく少なくする』なので、すべてのボタンを押してから、押さないボタンを探すことにします。
スイッチは奇数回（１回、３回、５回）切り替わるとＯＮになりライトが点灯し、偶数回（０回、２回、４回）切り替わるとＯＦＦでライトは消えます。…（★）
また、ボタンは押す場所だけが問題であり、ボタンを押す順番はどうでもいいことはわかりますね。
押すボタンは２４箇所ありますが、対称性に注意すると、５箇所について調べれば十分です。
全部のボタンを押す場合、下の図で同じ色に塗られた部分は必ず同じ回数だけスイッチが切り替わるはずです。
その５箇所は、それぞれ次のようにスイッチが切り替わります。
直接そのボタンを押したり、あるいはとなりあったボタンを押したときにスイッチが切り替わります。
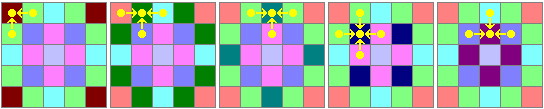
よって、すべてのボタンを押すと、スイッチの切り替わる回数は次のようになります。
ボタンにカラーで書いてある数字がスイッチの切り替わる回数です。
→（★）よりライトの点灯状況は→
となります。
ここまでくれば、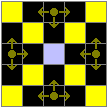
←図の●印をつけた４箇所を押さなければ、すべてのライトが点灯するということは容易にわかりますよね！
というわけで、問題図１の番号と照らし合わせて、３，１１，１４，２２が押さないボタンの番号です。
しかし、これが答えであると言うには、「押さないところが４箇所未満の場合はすべてのライトを点灯させられない」ことを示す必要があります。
これは、図で●印は４箇所あり、どこかのボタンを１回押さないだけで●印の２箇所（以上）のライトを点灯させることができないことからです。…（★）
さて、残った課題は、４箇所だけを押さないようにしてすべてのライト点灯させる方法は他にないのかということですが、結論からいうとありません。
その理由を以下に述べておきましょう。長くてわかりにくいだけの文ですが...(T_T)
（★）より、●印が４箇所あることから、押さないようにする４箇所はともに●印を必ず点灯させるような位置、つまり●印自体か、またはそれととなりあうボタンを押す必要があります。 …（☆）
（☆）の条件を満たすようなボタンのどこを押さないようにしてもON/OFFが切り替わるのは４箇所です。つまり、１回押さないごとに最高でも４箇所しか点灯させることができません。４回押す場合は、点灯できるのは最高でも１６箇所です。
一方、点灯させなければいけないボタンは全部で１６箇所あります。よって、無駄はまったく許されません。
●印以外の部分を押さないとすると４箇所も点灯させることはできない（逆に消灯してしまう箇所がある）ので、結局●印を押さないようにするほかありません。
（参考）なお、『なるべく多くのボタンを押す』という条件を省いた場合、次のように押してもすべてのライトを点灯させることができます。
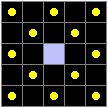
| 正解；３，１１，１４，２２ |