![]() 問28の解答
問28の解答
<解説>
かなりの難問といえるでしょう。
算数・数学に詳しい人であれば、「最短距離は直線・折れ線の最小値は折り返して直線に」の原則は問題を見た瞬間に思い浮かんだことでしょう。
ところが、この問題はそれだけではロープの長さを最短にする方法を特定することはできません。
まずは最短距離問題の定石通り、図形を折り返して考えます。
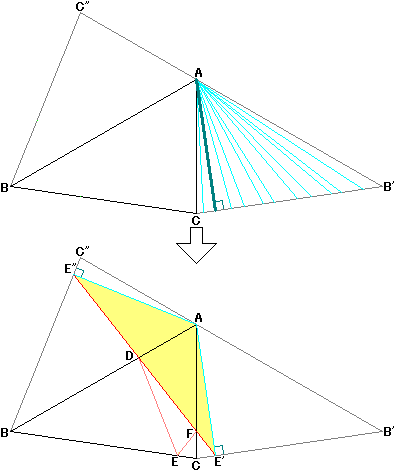
三角形ABCをACを軸として折り返すとき、移動後のBをB'そしてEをE'、三角形ABCをABを軸として折り返すとき、移動後のCをC"そしてEをE"とします。
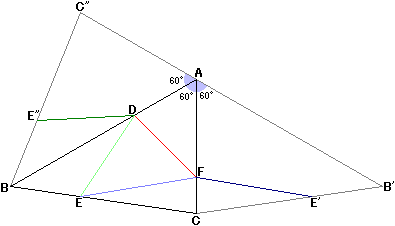
このとき、Eの位置にかかわらず、対称性よりFE=FE'、DE=DE"となります。
ということは、ロープの長さの和つまりEF+FD+DEは、E'F+FD+DE"の長さの和に等しくなります。
では、E'F+FD+DE"の長さを短くするにはどうしたらいいのでしょうか?
それは「E"からE'まで行くのに遠回りや寄り道をしなければよい」ということになります。
つまり、E"とE'の2点を直線で結べばOK!というわけです。
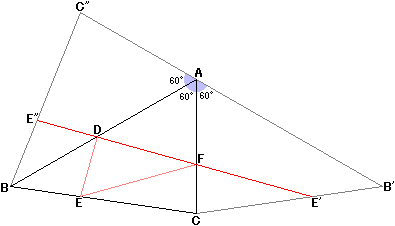
しかし、この問題はここで終わりではありません。
今まではEの位置をまったく議論していません。
EをBC上のどこに取るかによって、E"とE'の2点を直線で結ぶ方法というのはいくらでも考えられます。
よって、今度はその中でもロープの長さを最短にできるEの位置を考えます。
ただE"とE'を直線で結んだだけの図をにらんでいても、最短になるようなものは見当もつかないでしょう。
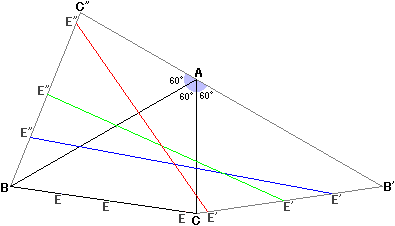
そんなときには迷わず補助線を引いてみよう、というわけで、AとE'、AとE"をともに直線で結んでみます。
三角形ACE'と三角形AC"E"は合同です。これはAC=AC"、CE'=C"E"、角ACE'=角AC"E"より、2辺とその間の角がそれぞれ等しいからですが、まぁこれに関しては直感でも明らかでしょう。
合同な三角形の対応する角度や辺の長さは等しいので、角E'AC=角E"AC"、AE'=AE"となります。
ここで、角E'AE"=角E'AC+角CAB+角BAE"=角CAB+角BAE"+角E"AC"ですが、角CAB=60度、そして角BAE"+角E"AC"=角BAC"=60度なので、角E'AE"=120度となります。
さらに、AE'=AE"ですから、三角形AE"E'は、Eの位置によらず、等しい2辺からなる内角が120度の二等辺三角形となります。
つまり、AE"E'は常に相似なんです。
よって、AE'の長さが最短のとき、E"E'の長さも最短になります。
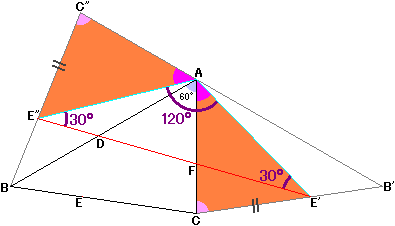
AE'の長さを最短にするには、Aと辺CB'の距離が最も短い位置にE'を取ればいいことになります。
つまり、AE'とCB'が直角をなすとき、AE'の長さは最短になり、同時にE"E'の長さも最短になります。
このとき、DとFの位置も決定しますね。
さて、あと一息ですが、ロープの長さを求めるのがやはりちと難しい。
中学入試ではすっかりお馴染みの「30度定規」の形を利用しますが、一工夫必要です。
※以下、点D、E、F、E'、E"は、ロープの長さが最短の位置にある場合を考えています。
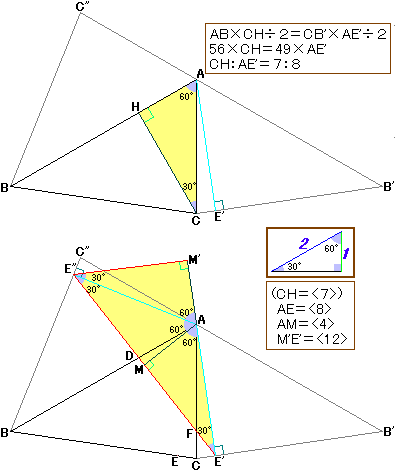
まずCからABに向けて垂線を引き、その足をHとします。 …(☆)
このとき三角形ABCの面積は、 AB×CH÷2 や CB'×AE'÷2 といった表し方があります。
これより、56×CH=49×AE'となるので、CH:AE'=7:8とわかります。
次に、E"E'の真ん中の点をMとし、AE"を軸として三角形AE"Mを折り返し、三角形AE"M'を作ります。
すると、角M'E"E'=30度×2=60度です。
また、AE'=<8>とすると、AM=<4>=AM'ですから、E'M'=<12>となります。 (ついでに、CH=<7>です)
さてここで、三角形CAHと三角形E'E"M'はともに「30度定規」の形なので相似です。
この2つの三角形について比例式を作ると、
AC:CH=E"E':E'M' … 35:<7>=E"E':<12>
となりますから、E"E'=35×12/7=60m=ロープの長さ と求まります。
[発展事項]
(☆)のとき、実は点Dと点Hは一致します。同様に、BからACに向けて引いた垂線の足と点Eは一致します。
これは、すべての鋭角三角形(=内角がすべて90度より小さい三角形)について言えます。
このことから、鋭角三角形の場合において、ロープの長さを最短にする方法は、三角形の各頂点から下ろした垂線の足を結んでできる三角形を作ればいいということになります。
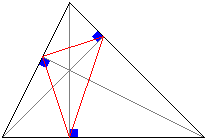
| 正解;60m |